고전역학에서 사용하는 천체의 위치 벡터나 운동량 벡터는 입자가 차지하고 있는 한 점에 정의된 벡터라는 점으로부터 앞에서 설명한 tangent vector라고 할 수 있다. 이와는 다르게 전자기학에서 사용하는 전기장, 자기장과 같은 개념들은 공간의 각 점마다 vector가 정의된 vector field의 개념이다. 본 포스팅에서는 manifold에서 vector field를 정의한다.
Vector Field
Vector field를 엄밀히 정의하기 위해서는 위상수학의 fiber bundle의 개념을 사용하여 정의해야 하지만, differentiable manifold의 개념들이 이미 정의되어 있으므로 이들을 이용하여 더 쉽게 정의할 수 있다.
Differentiable manifold \(M\)로부터 tangent bundle \(TM\)으로의 함수
$$ \begin{eqnarray} X & : & M & \to & TM \\ \\ & & p & \mapsto & X(p) := X_p \in T_pM \end{eqnarray} $$
를 \(M\)의 vector field라고 한다.
\(M\)의 모든 vector field들의 집합을 \(\mathfrak{X}(M)\)으로 표기한다.
$$ \mathfrak{X} = \{ X:M\to TM ~|~ X(p)=X_p \in T_pM \} $$
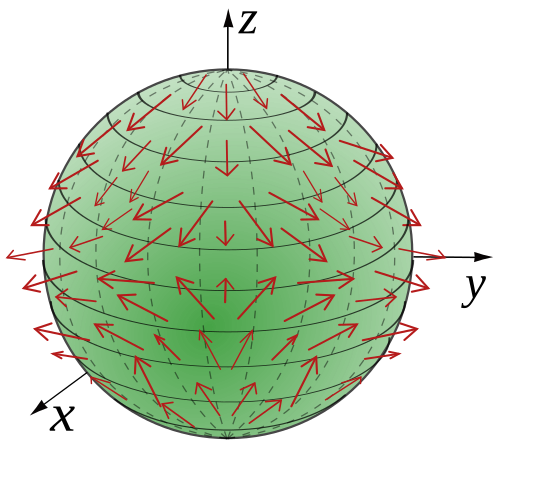
다음 그림은 구표면 \(S^2\)에 정의되는 vector field의 예이다.
I, Cronholm144 [GFDL, CC-BY-SA-3.0 or CC BY-SA 2.5 ], from Wikimedia Commons
만약 \(X\)가 differentiable map이면 vector field를 differentiable하다고 부른다.
Local coordinate \((U,\varphi)\)에서 vector field \(X\)는
$$ \hat{X}(x^1,\cdots,x^n)=\left(x^1,\cdots,x^n,~\hat{X}^1(x^1,\cdots,x^n)~,\cdots,~\hat{X}^n(x^1,\cdots,x^n)~\right) $$
로 표현된다. (앞으로 \(\hat{f}\)를 \(f\)의 local coordinate 표현 \(\hat{f}=f\circ \varphi\)로 정의한다.) 만약 \(X\)가 differentiable하다면, coefficient 함수 \(X^i : \varphi(U)\to \mathbb{R}\)가 differentiable이어야 한다. 역으로 \(X^i\)가 differentiable이라면 \(X\)도 differentiable이다.
Directional Derivative
1.3 Tangent Space, Tangent Bundle의 결론과 같이 tangent vector는 differentiable real-valued function의 1차 미분연산자이므로, vector field \(X\), differentiable real-valued function \(f\)에 대하여, \(X\cdot f:M \to \mathbb{R}\)를 정의할 수 있다. 이를 directional derivative라고 부른다.
Differentiable manifold \(M\)의 vector field \(X\)와 differentiable real-valued function \(f\)에 대하여, 함수 \(X\cdot f:M\to \mathbb{R}\)를 \(f\)의 \(X\)방향으로의 directional derivative라고 부른다. local coordinate에서 \(X=\sum_{i=1} ^n X^i \frac{\partial}{\partial x^i}\)라고 한다면,
$$ X \cdot f = \sum_{i=1} ^n X^i \frac{\partial \hat{f}}{\partial x^i} $$
이 된다.
Lie Bracket
\(X\), \(Y\)를 local coordinate에서
$$ X = \sum_{i=1} ^n X^i \frac{\partial}{\partial x^i} $$
$$ Y = \sum_{i=1} ^n Y^i \frac{\partial}{\partial x^i} $$
인 vector field라고 하자. 이제 두 vector field의 결합 \(X \circ Y\)를 생각할 수 있다. 그러나 \(X \circ Y\)는 vector field가 되지 못한다. local coordinate에서 볼 수 있는것과 같이
$$ (X\circ Y) \cdot f = X(Y\cdot f) = X\cdot \left( \sum_{i=1} ^n Y^i \frac{\partial \hat{f}}{\partial x^i} \right) = \sum_{i,j=1} ^n X^j \frac{\partial Y^i}{\partial x^j} \frac{\partial \hat{f}}{\partial x^i} + X^jY^i \frac{\partial^2 \hat{f}}{\partial x^i} $$
real-valued function에 대한 2차 미분을 포함하고 있기 때문에 vector field가 되지 못한다. 하지만, \(X \circ Y - Y \circ X\)는 1차 미분만을 포함하고 있기 때문에 vector field가 된다.
Differentiable manifold \(M\)의 vector field \(X\), \(Y\), 그리고 임의의 differentiable function \(f\)에 대하여
$$ Z\cdot f = (X\circ Y - Y\circ X) \cdot f $$
을 만족하는 vector field \(Z\)가 존재한다.
위 정리로부터 두 vector field를 이용해 정의된 새로운 vector field를 Lie bracket이라고 부른다.
Differentiable manifold \(M\)의 vector field \(X\), \(Y\)에 대하여, vector field
$$ [X,Y] = X \circ Y - Y \circ X $$
를 \(X\)와 \(Y\)의 Lie bracket이라고 부른다. Local coordinate에서
$$ [X,Y] = \sum_{i=1} ^n \left( \sum_{j=1} ^n X^j \frac{\partial Y^i}{\partial x^j} - \sum_{j=1} ^n Y^j \frac{\partial X^i}{\partial x^j} \right) \frac{\partial}{\partial x^i} $$
만약 \([X,Y]=0\)이면, \(X\)와 \(Y\)를 commute하다고 한다. Lie bracket은 다음과 같은 성질을 가지고 있다.
Vector field \(X\), \(Y\), \(Z\)에 대하여,
1. Bilinearity: 임의의 \(\alpha\), \(\beta \in \mathbb{R}\)에 대하여,
$$ [\alpha X+ \beta Y,Z] = \alpha [X,Z] + \beta [Y,Z] $$
$$ [X, \alpha Y+\beta Z] = \alpha [X,Y] + \beta [X,Z] $$
2. Alternativity:
$$ [X,X]=0 $$
3. Jacobi identity:
$$ [X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0 $$
4. Leibniz rule: 임의의 differentaible real-valued function \(f\), \(g\)에 대하여,
$$ [fX,gY] = fg[X,Y] + f(X\cdot g) Y - g(Y\cdot f)X $$
가 성립한다.
Vector field의 Lie bracket은 Lie group 이론의 Lie algebra의 일종이다. 일반적으로 Lie algebra는 1, 2, 3으로 정의되는 연산이며, 4번 성질은 vector field가 미분연산자이기 때문에 생기는 성질이다. 자세한 것은 --lie algebra--에서 다룬다.
Pushfoward
Differentiable manifold \(M\)과 \(N\)이 서로 diffeomorphic할 경우, \(M\)과 \(N\)은 manifold 관점에서 동일하기 때문에 \(M\)의 vector field \(X\)는 diffeomorphism에 의하여 자연스럽게 \(N\)의 vector field로 대응된다. 이렇게 diffeomorphism에 의하여 얻어지는 \(N\)의 vector field를 pushforward라고 부른다.
Differentiable manifold \(M\)과 \(N\)의 diffeomorphism을 \(\varphi:M\to N\)이라고 하고, \(X\)를 \(M\)의 vector field라고 하자. \(N\)의 vector field \(\varphi_\ast X\)를 다음과 같이 정의한다.
$$ (\varphi_\ast X)_p = (d\varphi)_{\varphi^{-1}(p)}X_{\varphi^{-1}(p)} \mathrm{~~~for~~} p \in N $$
이를 \(X\)의 pushforward라고 부른다.
경우에 따라 \(\varphi_\ast\) 대신 \(d\varphi\)로 표현하기도 한다.
By User:Fropuff~commonswiki [Public domain], via Wikimedia Commons
위의 그림과 같이 \(M\)과 \(N\)이 \(\varphi\)를 통해 diffeomorphic하다면, \(TM\)과 \(TN\)은 \(\varphi_*\)
를 통해 diffeomorphic하다. (\(\pi_M\)은 tangent vector가 정의되는 각 점으로 보내는 함수이다. 즉, \(TM\)의 원소 \((q,X_q)\)를 \(\pi_M(q,X_q)=q\)로 보내는 함수이다.)
Lie bracket의 pushforward는 각 vector field의 pushforward들의 Lie bracket과 같다.
$$ \varphi_\ast [X,Y] = [\varphi_\ast X , \varphi_\ast Y] $$
이를 확인하기 위해서 \(M\)의 local coordinates를 \(x\), \(N\)의 local coordinates를 \(y\)라고, vector field의 local coordinates 표현을
$$ X = \sum_{i=1} ^m X^i \frac{\partial}{\partial x^i} $$
$$ Y = \sum_{i=1} ^m Y^i \frac{\partial}{\partial x^i} $$
라고 하면,
$$ \varphi_\ast X = \sum_{i=1} ^m \sum _{j=1} ^n X^i \frac{\partial \hat{\varphi}^j}{\partial x^i} \frac{\partial}{\partial y^j} $$
$$ \varphi_\ast Y = \sum_{i=1} ^m \sum _{j=1} ^n Y^i \frac{\partial \hat{\varphi}^j}{\partial x^i} \frac{\partial}{\partial y^j} $$
'Mathematics > 다양체(텐서)' 카테고리의 다른 글
| [다양체,텐서] 1.8 Orientability (0) | 2018.09.08 |
|---|---|
| [다양체,텐서] 1.7 Submanifold (0) | 2018.08.18 |
| [다양체, 텐서] 1.6 Integral Curve (0) | 2018.08.18 |
| [다양체,텐서] 1.4 Derivatives of Differentiable maps (0) | 2018.08.11 |
| [다양체,텐서] 1.3 Tangent Space, Tangent Bundle (4) | 2018.08.07 |
| [다양체,텐서]1.2 Differentiable Maps, Diffeomorphism (4) | 2018.08.07 |