컴퓨터 공학, 물리학, 화학, 경제학 등에서 종종 언급되는 랜덤 워크는 말 그대로 방향을 임의로 정해서 움직이는 stochastic process를 의미한다. 먼저 가장 간단한 형태의 랜덤 워크를 이해해보자.
한 사람이 다음 그림과 같이 길게 연결된 N개의 점 위에서 시간이 지날때마다 왼쪽 또는 오른쪽으로 움직이는 상황을 생각해보자. \(t\) 시점에 이 사람이 있는 위치를 \(X_t\) 라고 하자. 예를 들어 \(X_3=N-2\) 는 \(t=3\) 시점에 이 사람이 서있는 곳이 \(N-2\)라는 뜻이다.

이 사람이 \(t\) 시점에 \(i\) 위치에 있었을 때, \(t+1\) 시점에는 왼쪽으로 이동, 즉 \(i-1\) 위치에 있을 확률이 1/2, 오른쪽으로 이동, 즉 \(i+1\) 위치에 있을 확률이 1/2이다. 즉, transition probability \(p(i,i-1) = \frac{1}{2}\), \(p(i,i+1) = \frac{1}{2}\) 이다.
이렇게 왼쪽, 오른쪽으로 이동하다가 왼쪽이나 오른쪽 끝에 도달하게 되면, 더 멀리 갈 수 있는 방향이 없기 때문에 새로운 이동 룰이 필요하다. 먼저, 아래 그림과 같이 무조건 반대 방향으로 이동하게 되는 상황을 생각해보자.
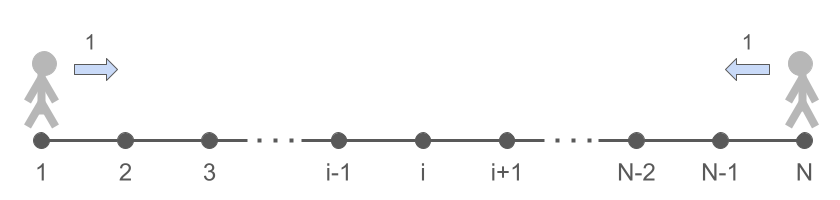
왼쪽 또는 오른쪽 끝의 transition probability는 \(p(1,2) = 1\), \(p(N,N-1)=1\) 이다. transition probability를 종합하면 다음과 같다:
\[ \begin{align} p(i,i+1) &= \frac{1}{2} &\text{if } 1 < i < N \\ \\ p(i,i-1) &= \frac{1}{2} &\text{if } 1 < i < N \\ \\ p(0,1) &= 1, &p(N,N-1) = 1 \\ \\ p(i,j) &=0 &\text{for other }i, j \end{align} \]
따라서 transition matrix는 다음과 같은 형태가 된다.
\[ \begin{bmatrix} 0 & 1 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 \\ \frac{1}{2} & 0 & \frac{1}{2} & 0 & \cdots & 0 & 0 & 0 & 0 \\ 0 & \frac{1}{2} & 0 & \frac{1}{2} & \cdots & 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \\ 0 & 0 & 0 & 0 & \cdots & \frac{1}{2} & 0 & \frac{1}{2} & 0 \\0 & 0 & 0 & 0 & \cdots & 0 & \frac{1}{2} & 0 & \frac{1}{2} \\ 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 1 & 0 \end{bmatrix} \]
이러한 이동을 symmetric random walk with reflecting boundaries라고 부른다. symmetric은 왼쪽, 오른쪽으로 이동할 확률이 서로 같다는 뜻이다. 만약 왼쪽과 오른쪽 이동 확률이 서로 다르다면 biased random walk라고 부른다. reflecting boundary는 말 그대로 끝에 도달하면 반사해서 반대 방향으로 이동한다는 뜻이다.
만약 끝에 도달했을 때 더 이상 이동하지 않고 그 자리에 멈추는 경우도 생각할 수 있다. 이러한 것을 absorbing boundary라고 부른다.
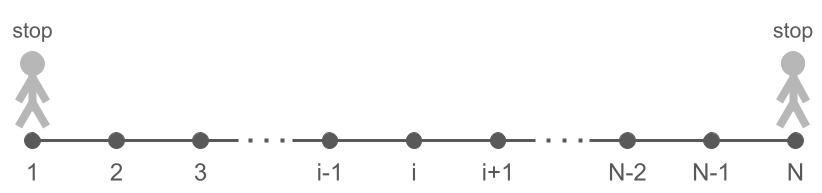
이 경우 transition probability는 다음과 같이 바뀐다.
\[ \begin{align} p(i,i+1) &= \frac{1}{2} &\text{if } 1 < i < N \\ \\ p(i,i-1) &= \frac{1}{2} &\text{if } 1< i < N \\ \\ p(0,0) &= 1, &p(N,N)=1 \\ \\ p(i,j) &=0 &\text{for other } i,j \end{align} \]
즉, transition matrix는 다음과 같이 바뀐다.
\[ \begin{bmatrix} 1 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 0 \\ \frac{1}{2} & 0 & \frac{1}{2} & 0 & \cdots & 0 & 0 & 0 & 0 \\ 0 & \frac{1}{2} & 0 & \frac{1}{2} & \cdots & 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \\ 0 & 0 & 0 & 0 & \cdots & \frac{1}{2} & 0 & \frac{1}{2} & 0 \\0 & 0 & 0 & 0 & \cdots & 0 & \frac{1}{2} & 0 & \frac{1}{2} \\ 0 & 0 & 0 & 0 & \cdots & 0 & 0 & 0 & 1 \end{bmatrix} \]
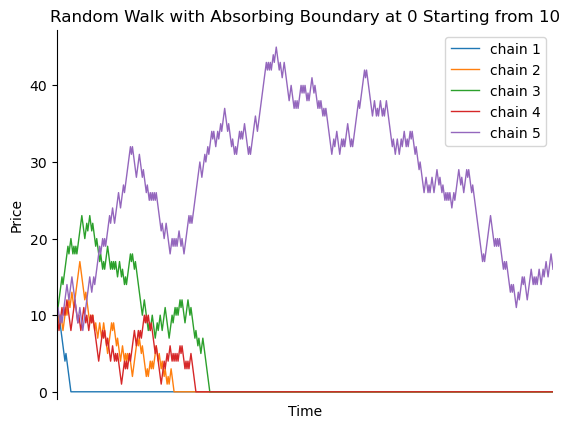
특히 absorbing boundary는 포트폴리오의 가치를 random walk로 기술하고자 할 때 중요한데, 포트폴리오의 가치가 계속 변하다가 파산 지점에 도달하는 경우에는 가치가 영원히 0이 되는 상황을 모델링 할 수 있다. 파산을 고려하지 않은 상태에서 이익을 가져올 것이라고 생각했던 전략이 파산까지 고려하면 오히려 위험한 전략이라는 것을 발견할 수 있다. 가장 잘 알려진 전략이 마팅게일 베팅 전략이다. 동전 던져서 앞면인지 뒷면인지 맞추는 게임을 한다고 하자. 동전을 던지기 전에 판돈을 베팅하는데, 어느 면인지 맞추면 판돈만큼 이익을 보고, 틀리면 판돈을 잃는 다고 하자. 먼저 1원을 앞면에 걸었다고 해보자. 만약 동전을 던져서 앞면이 나오면 1원을 벌었으니 OK. 만약 뒷면이 나왔다면, 이제 2원을 앞면에 건다. 다시 동전을 던져서 앞면이 나오면 2원을 벌어서 앞에서 손해본 1원을 빼면 다시 1원을 벌었으니 OK. 다시 뒷면이 나왔으면, 다시 4원을 앞면에 건다. 여기에서 앞면이 나오면 4원을 벌었으니 앞에서 총 손해 3원을 빼면 1원을 번게 된다. 이런 식으로 \(n\)번째에 앞면이 나왔다고 한다면,
\[ \text{손해} = \sum _{i=1} ^{n-1} 2^{i-1} = 2^n - 1\]
이므로, 항상 1원의 이득이 생긴다. 그러나 현실에서는 내가 가진 돈이 0원이 되는 순간 더이상 게임을 지속할 수 없어 손실이 발생하게 된다.1
더 일반적인 random walk는 graph에서의 random walk를 생각할 수 있다.

각 점에서 다음 점으로 연결된 지점으로만 갈 수 있고, 이 때의 확률은 1/시작점에 연결된 선 개수 이다. 예를 들어 1에서 2로 이동할 확률은, 1에 연결된 선이 3개이므로 1/3이다. 이 graph에서 random walk의 transition matrix는
\[ \begin{bmatrix} 0 & \frac{1}{3} & 0 & \frac{1}{3} & 0 & \frac{1}{3} & 0 & 0 \\ \frac{1}{3} & 0 & \frac{1}{3} & \frac{1}{3} & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ \frac{1}{3} & 0 & 0 & 0 & \frac{1}{3} & 0 & \frac{1}{3} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2} & 0 & \frac{1}{2} \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \end{bmatrix} \]
가 된다.
- 더 자세한 이론적 배경은 (페이지 추가 후 링크 추가) [본문으로]
'Etc > 확률 과정' 카테고리의 다른 글
| [확률과정] 1.3-(2) Example: Queueing Model (1) (1) | 2024.01.10 |
|---|---|
| [확률과정] 1.3 transition matrix (1) | 2024.01.01 |
| [확률과정] 1.2 Markov Chain (1) | 2023.12.31 |
| [확률과정] 1.1 Stochastic process (3) | 2023.12.31 |