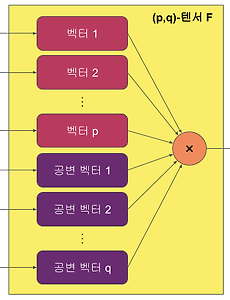
텐서란 무엇인가? 텐서의 이해, 표기법, 연산 완전 정리
물리학을 배우는 학생이라면 방학 중에 꼭 상대성이론 한번 공부해 보겠다고 책을 샀다가, 텐서에서 눈물을 머금고 포기하기를 반복하는 경험을 한번씩은 할 것이다. 그만큼 물리학과 학생에게 텐서는 애증의 개념이라고 할수 있다. 아마 텐서가 무엇인지, 텐서가 왜 필요한지에 대해서는 이런 저런 소스로부터 많이 봤을 것이니, 여기에서는 텐서의 핵심적인 특징과 표기법, 연산에 대하여 정리하여 실제적으로 텐서를 가지고 계산을 하는 방법들에 대하여 살펴본다. 먼저, 텐서를 이해하기 위해서는 다음의 개념들에 대해서는 반드시 알아야 한다. 1. 함수 : 함수의 기본 개념, 변수와 함수값, 벡터 함수 2. 스칼라와 벡터 : 스칼라와 벡터의 기본 개념, 벡터의 덧셈, 스칼라 곱, 벡터의 내적, 벡터의 내적의 성질 3. 벡터와 ..
2020. 8. 11.
[다양체,텐서] 2.2 Symmertric Tensors, Antisymmetric Tensors, Exterior Algebra
이 페이지에서는 앞으로 많이 등장하게 될 antisymmetric tensor들을 살펴본다. 그리고 비슷한 개념의 symmetric tensor도 같이 살펴본다. 논의의 편의상 covariant tensor만 다루지만, contravariant tensor에도 똑같은 방식으로 적용된다. 이하에서는 vector space \(V\)의 basis를 $$ \{ e_1, e_2, \cdots , e_n\} $$ 그리고 dual space \(V^*\)의 dual basis를 $$ \{ e^* _1, e^* _2, \cdots, e^* _n \} $$ 으로 가정한다. Symmetric Tensors Symmetric tensor는 변수로 들어가는 vector들 중에서 2개의 위치를 바꿨을 때 같은 값이 나오는 t..
2018. 9. 8.
