[다양체,텐서] 1.4 Derivatives of Differentiable maps

미적분학에서 '미분'이라는 개념은 linear approximation이라는 개념으로 설명된다.(--calculus, differential-- 참고)

$$\mathrm{\Delta }f=f(x+\mathrm{\Delta }x)-f(x)=d{f}_x(\mathrm{\Delta }x)+ϵ\mathrm{where}\frac{ϵ}{\mathrm{\Delta }x}\to 0\mathrm{as}\mathrm{\Delta }x\to 0$$

$\mathrm{\Delta }x$는 $\mathbb{R}$에서의 tangent vector라고 할 수 있으므로, differential $d{f}_x$는 tangent space에서 tangent space로의 linear transformation이라고 볼 수 있다.([선형대수학] 2.1 Linear Transformation 참고) 이러한 관점은 다변수 함수의 미분에서 Jacobian으로 일반화 된다. (--calculus, multi-var,differential-- 참고)

 

같은 방식으로 미적분학의 differnetial 개념은 differentiable manifold에서 선형 근사로 일반화된다.

 

DEFINITION            Pushforward (tangent vector)

 

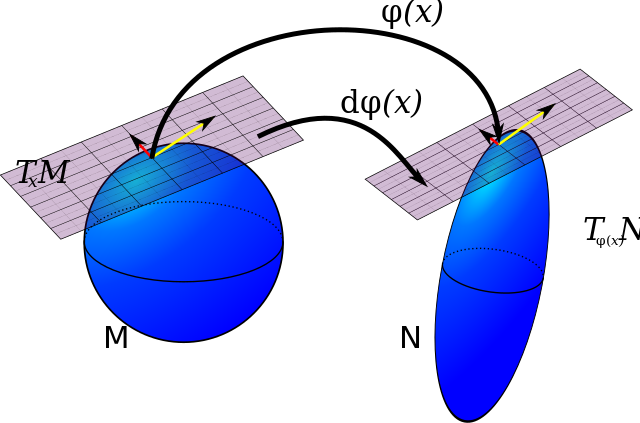
Differentiable manifold 사이의 함수 $\phi :M\to N$가 differentiable이라고 하자. $M$의 point $x$에 대하여, ($x$에서) $\phi$의 differential $d{\phi }_x$를 다음과 같은 linear transformation으로 정의한다.

$$\begin{array}{ccrcl}d{\phi }_x& :& T_{x}M& \to & T_{\phi (x)}N\\ & & v& \mapsto & \frac{d(\phi \circ c)}{dt}(0)\end{array},\mathrm{where}\mathrm{curve}c(0)=x\mathrm{and}\dot{c}(0)=v$$

이 때, tangent vector $v$로의 $d{\phi }_x$의 적용을 $\phi$에 의한 $v$의 pushforward라고 부른다.

 

위의 정의에서 differential $d{\phi }_x$는 tangent vector $v$에 대하여 위 조건을 만족하는 어떤 differentiable curve $c$을 선택하던지 똑같은 linear operator가 된다. 경우에 따라서 $d\phi$ 대신 ${\phi }_{\ast }$로 표현하기도 한다.

 

By User from reddit [CC BY 3.0 ], from Wikimedia Commons

 

 

$M$의 local coorindate $x$, $N$의 local coordinate $y$에 대하여, $p\in M$에서의 tangent vector $v$가

$$v=\sum _{i=1}^m{v}^i{\left(\frac{\partial }{\partial x^i}\right)}_p$$

라고 하면, ${\phi }_p\in N$에서의 tangent vector $d{\phi }_p(v)$는

$$d{\phi }_p(v)=\sum _{j=1}^n\left(\sum _{i=1}^m{v}^i{\frac{\partial }{\partial x^i}(y^j\circ f\circ x)|}_p\right)\left(\frac{\partial }{\partial y^j}\right)$$

가 된다.

 

 

미적분에서 자주 응용되는 chain rule은 다음과 같이 정리된다.

 

THEOREM            Chain Rule (differential)

 

$f:M\to N$, $g:N\to P$를 differentiable 함수라고 하자. 그러면 합성함수 $g\circ f:M\to P$도 differentiable이고,

$$(d(g\circ f){)}_p=(dg{)}_{f(p)}\circ (df{)}_p$$

이다.