미적분학에서 3차원 Euclidean space \(\mathbb{R}^3\)에서 surface의 한 점에 접하는 평면을 tangent plane이라고 부른다.
By Alexwright at English Wikipedia [Public domain], via Wikimedia Commons
이 페이지에서는 한 점에 대한 tangent plane이 differentiable manifold에서 일반화된 개념에 대하여 살펴본다.
Tangent Space
미적분학에서 plane을 표현하는 방법에는 여러가지 방식이 있다. 가장 익숙한 방식으로는 1차 2-변수 함수를 이용하여
$$ s(x,y)=x+y $$
와 같이 표현할 수 있다. 그러나 이러한 방식은 tangent plane이 3차원 Euclidean space의 subspace이기 때문에 surface보다 더 높은 차원인 3차원에서 접근할 수 있어야 가능한 방식이다.
또다른 방식으로 surface의 normal vector와 normal vector에 수직한 plane으로 표현하는 방식이다. Normal vector 역시 더 높은 차원을 가정해야 사용할 수 있는 개념이기 때문에 manifold에서 사용할 수 없지만, normal vector에 수직하여 plane에 속하는 vector들은 더 높은 차원을 가정하지 않고 surface만을 가지고 정의할 수 있다.(--미적분,normal vector-- 참고) Tangent plane을 일반화한 개념인 tangent space는 이러한 방식으로 정의된다.
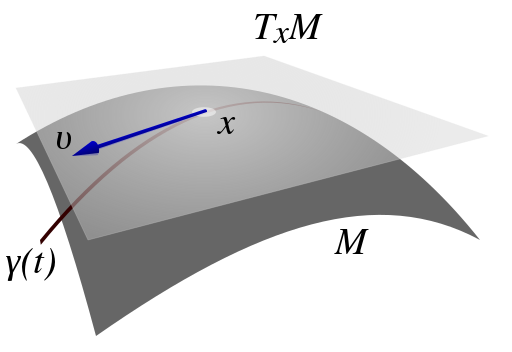
Differentiable manifold \(M\)에 정의되는 differentiable curve를 \(\gamma:(-\epsilon,\epsilon)\to M\)라고 하자. Point \(\gamma(0)=x \in M\)에서 curve \(\gamma\)의 tagent vector는 임의의 differentiable function \(f:M\to \mathbb{R}\)에 대하여 정의되는 미분 operator \(\dot{\gamma}(0)=v\)
$$ v(f) = \left. \frac{d}{dt}(f\circ \gamma)\right| _{t=0} $$
로 정의된다. Point \(x\)에서의 tangent vector들의 집합을 \(T_xM\)이라고 쓰고 \(x\)에서의 tangent space라고 부른다.
By derivative work: McSush (talk)Tangentialvektor.png: TNThe original uploader was TN at German Wikipedia. (Tangentialvektor.png) [Public domain],
\(x\)가 포함된 chart에서의 parametrization을 \(\varphi\)라고 하면,
$$ \varphi^{-1} \circ \gamma (t) = (x^1(t),...x^n(t)) $$
인 \(\mathbb{R}\to \mathbb{R}^n\) 함수라고 할 수 있고
$$ f \circ \varphi $$
도 \(\mathbb{R}^n\to\mathbb{R}\) 함수라고 할 수 있으므로
$$ \begin{eqnarray} v(f) & = & \left. \frac{d}{dt}(f\circ \gamma)\right|_{t=0} = \left. \frac{d}{dt}(f\circ \varphi \circ \varphi^{-1} \circ \gamma)\right|_{t=0} \\ & = & \frac{d}{dt}\left(f\circ \varphi \right)(x^1(t),x^2(t),\cdots,x^n) = \sum_{i=1} ^n \frac{\partial (f\circ \varphi)}{\partial x^i}\frac{dx^i}{dt}(0) \\ & = & \left( \sum_{i=1} ^n \dot{x}^i(0)\left(\frac{\partial}{\partial x^i}\right)_{\phi^{-1}(x)}\right)(f\circ \varphi) \end{eqnarray} $$
따라서 미분 operator \(\dot{\gamma}(0)\)는
$$ \dot{\gamma}(0) = \sum_{i=1} ^n \dot{x}^i (0) \left(\frac{\partial}{\partial x^i}\right)_p $$
로 표현된다. (이 때, \(\left(\frac{\partial}{\partial x^i}\right)_p\)는 curve
$$ \varphi^{-1} \circ \gamma_i (t) = \left(x^1,\cdots,x^{i-1},x^i+t,x^{i+1},\cdots,x^n\right) $$
의 tangent vector이다.)
\(T_xM\)의 원소를 tangent vector라고 부르는 이유는 \(T_xM\)이 vector space가 되기 때문이다. 만약 \(v,w \in T_xM\)이면,
$$ v(f) = \left. \frac{d}{dt}(f \circ \gamma)(0) \right| _{t=0} ~~,~~ \gamma(0) = x $$
$$ w(f) = \left. \frac{d}{dt}(f \circ \kappa)(0) \right| _{t=0} ~~,~~ \kappa(0) = x $$
를 만족하는 differentiable curve \(\gamma\), \(\kappa\)가 존재한다. 이제, vector \(s\)를
$$ \varphi^{-1} \circ \omega (t) = \varphi^{-1} \circ \gamma (t) + \varphi^{-1} \circ \kappa (t) $$
를 만족하는 differentiable curve \(\omega\)의 tangent vector로 정의하면,
$$ \begin{eqnarray} s(f) & = & \left. \frac{d}{dt}(f\circ \omega) \right| _{t=0} = \left. \frac{d}{dt}(f \circ \varphi \circ \varphi ^{-1} \circ \omega) \right| _{t=0} \\ & = & \left. \frac{d}{dt}(f \circ \varphi \circ (\varphi ^{-1} \circ \gamma + \varphi^{-1} \circ \kappa)) \right| _{t=0} \\ & = & \left. \frac{d}{dt}(f \circ \varphi \circ \varphi ^{-1} \circ \gamma) \right| _{t=0} + \left. \frac{d}{dt}(f \circ \varphi \circ \varphi ^{-1} \circ \kappa) \right| _{t=0} = v(f)+w(f) \end{eqnarray} $$
이므로 \(v+w=s \in TxM\)이다.
같은 방식으로
$$ \varphi^{-1} \circ \omega (t) = \lambda \cdot \varphi^{-1} \circ \gamma (t) $$
을 만족하는 diffrentiable curve \(\omega\)의 tangent vector는 \(\lambda\cdot v\)가 된다. 따라서
[선형대수학] 1.1 Vector Space의 vector space 공리를 만족한다.
즉, differentiable manifold에서 정의되는 vector는 (differentiable real-valued function의) 미분 연산자이다.
\(n\)-dimensional differentiable manifold \(M\)의 점 \(x\)에서의 tangent space는 \(n\)-dimensional vector space이다.
위의 논의에 따라, operator
$$ \left(\frac{\partial}{\partial x^1}\right)_x , \left(\frac{\partial}{\partial x^2}\right)_x , \cdots, \left(\frac{\partial}{\partial x^n}\right)_x $$
들은 \(T_xM\)의 basis가 된다. 따라서 임의의 tangent vector \(v\)는
$$ v = \sum_{i=1} ^n v^i \left( \frac{\partial}{\partial x^i} \right)_x $$
로 표현된다.
Example
\(S^2\)의 parametrization \(\psi : (0,\pi)\times (-\pi,\pi) \to S^2\)가
$$ \psi(\theta,\varphi) = (\sin\theta\cos\varphi,\sin\theta\sin\varphi,\cos\theta) $$
로 주어지는 경우 \(1,0,0\)에서의 basis vector \(\left( \frac{\partial}{\partial \theta}\right)_{(1,0,0)}\), \(\left( \frac{\partial}{\partial \varphi}\right)_{(1,0,0)}\)를 구해보자.
위의 논의로부터, curve
$$ \gamma (t) = \psi(\frac{\pi}{2}+t,0) = (\cos{t},0,-\sin{t}) $$
$$ \kappa (t) = \psi(\frac{\pi}{2},t) = (\cos{t},\sin{t},0) $$
를 잡으면, \(\mathbb{R}^3\)에서
$$ \left( \frac{\partial}{\partial \theta}\right)_{(1,0,0)} = \left( \frac{d}{dt} \gamma \right)_{t=0} = (0,0,-1) $$
$$ \left( \frac{\partial}{\partial \varphi}\right)_{(1,0,0)} = \left( \frac{d}{dt} \kappa \right)_{t=0} = (0,1,0) $$
이 된다.
Change of Basis
Point \(p\)가 chart \((U,\varphi)\)와 \((V,\psi)\)에 동시에 속하고
$$ \varphi^{-1} (p) = (x^1,x^2,\cdots,x^n) $$
$$ \psi^{-1} (p) = (y^1, y^2, \cdots, y^n) $$
이라고 하고, 위에서 사용한 표현대로 parametrization \(\varphi\)에서의 basis vector를 \( \left(\frac{\partial}{\partial x^i}\right)_p \), \(\psi\)에서의 basis vector를 \( \left(\frac{\partial}{\partial y^i}\right)_p \)로 표현하자.
이제 \(T_xM\)의 임의의 vector \(v\)가 \(\varphi\)의 parametrization에서
$$ v=\sum_{i=1} ^n v^i \left( \frac{\partial}{\partial x^i} \right)_p $$
표현되면, \( \left(\frac{\partial}{\partial x^i}\right)_p \)에 해당하는 differentiable curve \(\gamma_i\)가
$$ \varphi^{-1} \circ \gamma_i (t) = \left(x^1,\cdots,x^{i-1},x^i+t,x^{i+1},\cdots,x^n\right) $$
를 만족하므로
$$ \begin{eqnarray} \left( \frac{\partial}{\partial x^i} \right)_p(f) & = & \left( \frac{d}{dt} (f \circ \gamma_i) \right)_{t=0} = \left( \frac{d}{dt} (f \circ \psi \circ \psi^{-1} \circ \varphi \circ \varphi^{-1} \circ \gamma_i) \right)_{t=0} \\ & = & \sum_{j=1} ^n \left( \frac{\partial}{\partial y^j} (f \circ \psi) \frac{d}{dt}( (\psi^j)^{-1} \circ \varphi \circ \varphi^{-1} \circ \gamma_i) \right)_{t=0} \end{eqnarray} $$
이 때, \( \psi^{-1} \circ \varphi \)는 transition map이므로 differentiable이다. 따라서,
$$ \left( \frac{\partial}{\partial x^i} \right)_p(f) = \sum_{j=1} ^n \left( \frac{\partial}{\partial y^j} (f \circ \psi) \frac{\partial y^j}{\partial x^i} \right)_{t=0} $$
가 된다. 즉, parametrization \(\varphi\)와 \(\psi\)에서의 basis vector들 사이에는 다음과 같은 관계가 성립한다.
$$ \begin{bmatrix} \left(\frac{\partial}{\partial x^1} \right)_p \\ \left(\frac{\partial}{\partial x^2} \right)_p \\ \vdots \\ \left(\frac{\partial}{\partial x^n} \right)_p \end{bmatrix} = \begin{bmatrix} \left(\frac{\partial y_1}{\partial x^1} \right)_p & \left(\frac{\partial y_2}{\partial x^1} \right)_p & \cdots & \left(\frac{\partial y_n}{\partial x^1} \right)_p \\ \left(\frac{\partial y_1}{\partial x^2} \right)_p & \left(\frac{\partial y_2}{\partial x^2} \right)_p & \cdots & \cdots \\ \vdots & \ddots & \ddots & \vdots \\ \cdots & \cdots & \cdots & \left(\frac{\partial y_n}{\partial x^n} \right)_p \end{bmatrix} \begin{bmatrix} \left(\frac{\partial}{\partial y^1} \right)_p \\ \left(\frac{\partial}{\partial y^2} \right)_p \\ \vdots \\ \left(\frac{\partial}{\partial y^n} \right)_p \end{bmatrix} $$
이 때, 가운데 matrix는 함수 \(y:\mathbb{R}^n \to \mathbb{R}^n\)
$$ y(x^1,x^2,\cdots)= (y^1,y^2,\cdots,y^n) $$
의 Jacobian matrix임을 알 수 있다.
따라서,
$$ v=\sum_{j=1} ^n v'^j \left( \frac{\partial}{\partial y^j} \right)_p = \sum_{i=1} ^n v^i \left( \frac{\partial}{\partial x^i} \right)_p = \sum_{i=1} ^n v^i \left(\sum_{j=1} ^n \left( \frac{\partial y^j}{\partial x^i} \frac{\partial}{\partial y^j} \right)_p \right) $$
같은 표현으로,
$$ v' ^j = \sum_{i=1} ^n v^i \left( \frac{\partial y^j}{\partial x^i} \right)_p $$
를 만족한다.
Tangent Bundle
Tangent space는 manifold의 한 점에 정의되는 것이기 때문에 물리에서 다루는 vector field와 같이 여러 점에서의 vector와 미분, 적분을 다루기 위해서는 tangent bundle의 개념이 필요하다.
Differentiable manifold \(M\)에 대하여, tangent space의 disjoint union을 tangent bundle이라고 부르고 \(TM\)으로 표현한다.
$$ TM = \bigsqcup _{x\in M} T_xM = \bigcup _{x\in M} \{x\} \times T_xM = \{ (x,y)~|~ x\in M , y \in T_xM \} $$
By Oleg Alexandrov [Public domain], via Wikimedia Commons
각 점에서의 tangent space는 그림에서 보는 것과 같이 접하는 그 점에 접하는 space로 이해할 수 있다. 아래 그림처럼 각 space가 겹치치 않는 union이 tangent bundle의 개념이다. (그림에서 보는바와 같이 실제로, \(S^1\)의 tangent bundle은 무한한 높이의 cylinder이다. \(TS^1 \cong S^1\times \mathbb{R}\))
\(TM\) 역시 differentiable manifold가 된다. \(n\)-dimensional differentiable manifold \(M\)의 atlas를 \(\{(U_\alpha, \varphi_\alpha)\}\)라고 하면, 함수
$$ \begin{eqnarray} \Phi _\alpha & : & U_\alpha \times \mathbb{R}^n & \to & TM \\ & & (x,v) & \mapsto & (d\varphi_\alpha)_x(v) \in T_{\varphi_{\alpha (x)}}M \end{eqnarray} $$
로 잡으면, \(\{(U_\alpha \times \mathbb{R}^n, \Phi_\alpha)\}\)는 \(TM\)의 atlas가 된다. 따라서 \(TM\)은 \((2n)\)-dimensional differentiable manifold이다. (\((d\varphi_\alpha)_x\)는 1.4 Derivatives of Differentiable maps 참고)
'Mathematics > 다양체(텐서)' 카테고리의 다른 글
| [다양체,텐서] 1.7 Submanifold (0) | 2018.08.18 |
|---|---|
| [다양체, 텐서] 1.6 Integral Curve (0) | 2018.08.18 |
| [다양체,텐서] 1.5 Vector Fields, Lie Bracket (3) | 2018.08.12 |
| [다양체,텐서] 1.4 Derivatives of Differentiable maps (0) | 2018.08.11 |
| [다양체,텐서]1.2 Differentiable Maps, Diffeomorphism (4) | 2018.08.07 |
| [다양체,텐서] 1.1 Differentiable Manifolds (12) | 2018.08.06 |