텐서란 무엇인가? 텐서의 이해, 표기법, 연산 완전 정리

물리학을 배우는 학생이라면 방학 중에 꼭 상대성이론 한번 공부해 보겠다고 책을 샀다가, 텐서에서 눈물을 머금고 포기하기를 반복하는 경험을 한번씩은 할 것이다. 그만큼 물리학과 학생에게 텐서는 애증의 개념이라고 할수 있다. 아마 텐서가 무엇인지, 텐서가 왜 필요한지에 대해서는 이런 저런 소스로부터 많이 봤을 것이니, 여기에서는 텐서의 핵심적인 특징과 표기법, 연산에 대하여 정리하여 실제적으로 텐서를 가지고 계산을 하는 방법들에 대하여 살펴본다.

먼저, 텐서를 이해하기 위해서는 다음의 개념들에 대해서는 반드시 알아야 한다.

1. 함수 : 함수의 기본 개념, 변수와 함수값, 벡터 함수

2. 스칼라와 벡터 : 스칼라와 벡터의 기본 개념, 벡터의 덧셈, 스칼라 곱, 벡터의 내적, 벡터의 내적의 성질

3. 벡터와 공변벡터 : 공변벡터의 기본적인 개념

함수, 스칼라, 벡터, 공변벡터에 대해서 잘 모른다면 텐서를 이해할 준비가 덜 된 것이니 개념들을 알아보고 다시 도전하자.

#벡터와 공변벡터의 기본 연산

아마 텐서에 대해서 이것저것 찾아보면 벡터와 공변벡터에 대해서 여러가지 개념들이 나올것이다. 공변벡터에 대하여 여러가지 설명들이 많이 봤을 것으로 가정하고, 먼저 벡터와 공변벡터를 수학적으로 표기하는 것부터 시작하자.

NOTATION 벡터, 공변벡터

벡터 $v$ 는 $\vec{v}$ , 공변벡터 $w$ 는 $\underset{―}{w}$ 로 쓰기로 한다.

벡터와 공변벡터의 핵심적인 내용은 서로 내적 연산이 가능하다는 것이다.

$[\begin{matrix} 1 \\ 2 \\ 3 \end{matrix}]$

와 열벡터(공변벡터)

$[\begin{matrix} 1 & 2 & 3 \end{matrix}]$

는 서로 내적하여

$[\begin{matrix} 1 & 2 & 3 \end{matrix}] [\begin{matrix} 1 \\ 2 \\ 3 \end{matrix}] = 14$

를 얻을 수 있다. 물리학에서는 벡터 $r$ 와 공변벡터 $\nabla V$ 의 내적 $\nabla V \cdot r$ 을 하면 스칼라가 나옴을 알 수 있다. 즉, 벡터와 공변벡터는 서로 내적하여 스칼라가 나온다. 이를 함수를 이용하여 다음처럼 이해할 수도 있다.

공변벡터: 벡터가 들어가면 스칼라(벡터와 공변벡터의 내적값)이 나오는 함수

벡터: 공변벡터가 들어가면 스칼라(벡터와 공변벡터의 내적값)이 나오는 함수

따라서 벡터와 공변벡터의 내적을 함수와 같이 표기할 수 있다.

NOTATION 벡터와 공변벡터의 연산

벡터 $\vec{v}$ 와 공변벡터 $\underset{―}{w}$ 의 내적을 다음과 같이 표기한다.

$\underset{―}{w} (\vec{v})$ 또는 $\vec{v} (\underset{―}{w})$

함수의 개념처럼 $\underset{―}{w} (\vec{v})$ 는 $\underset{―}{w}$ 에 $\vec{v}$ 가 들어가는 것(위쪽 그림)을 표현하고, $\vec{v} (\underset{―}{w})$ 는 $\vec{v}$ 에 $\underset{―}{w}$ 가 들어가는 것(아래쪽 그림)을 표현한다.

또 다른 표기 방법으로는 벡터와 공변벡터의 성분을 이용하는 표기하기도 한다. 벡터 $\vec{v}$ 의 첫번째 성분을 $v^{1}$ , 두번째 성분을 $v^{2}$ ... 와 같이 벡터의 성분은 위 첨자를 이용한다. 공변벡터 $\underset{―}{w}$ 의 첫번째 성분을 $w_{1}$ , 두번째 성분을 $w_{2}$ ... 와 같이 공변벡터의 성분은 아래 첨자를 사용한다. 그러므로 행벡터와 열벡터(공변벡터)의 내적

$[\begin{matrix} w_{1} & w_{2} & \dots & w_{n} \end{matrix}] [\begin{matrix} v^{1} \\ v^{2} \\ ⋮ \\ v^{n} \end{matrix}] = w_{1} v^{1} + w_{2} v^{2} + \dots + w_{n} v^{n} = \sum_{i = 1}^{n} w_{i} v^{i}$

와 같이 표현된다. 따라서 내적 연산을 다음과 같이 표기하기도 한다.

NOTATION 벡터와 공변벡터, 연산의 성분표현

벡터 $\vec{v}$ 대신 i번째 성분 $v^{i}$ , 공변벡터 $\underset{―}{w}$ 대신 j번째 성분 $w_{j}$ 로 표현할 수 있다.^[각주:1] 따라서 $\vec{v}$ 와 $\underset{―}{w}$ 의 내적은 다음과 같이 표현할 수 있다.

$w_{i} (v^{i})$ 또는 $v^{i} (w_{i})$

또는 $\sum_{i = 1}^{n} w_{i} v^{i}$ 에서 $\sum_{i = 1}^{n}$ 을 생락하고

$w_{i} v^{i}$ 또는 $v^{i} w_{i}$

와 같이 표현한다.^[각주:2] 내적하는 벡터와 공변 벡터의 인덱스는 똑같은 문자를 사용한다.

기억해야 할 것은, 벡터와 공변벡터의 내적연산은 스칼라가 나온다는 것이다.

#선형 함수와 텐서

텐서에 대해 설명하기 전에 마지막으로 필요한 내용이 선형 함수에 대한 내용이다.

DEFINITION 선형 함수

벡터를 변수로 하는 함수 $f$ 가 다음을 항상 만족하는 경우 $f$ 를 선형 함수라고 부른다.

$f ({\vec{v}}_{1} + {\vec{v}}_{2}) = f ({\vec{v}}_{1}) + f ({\vec{v}}_{2})$

$f (c \cdot \vec{v}) = c \cdot f (\vec{v})$

이 조건을 하나로 합쳐서 다음과 같이 표현하기도 한다.

$f (c {\vec{v}}_{1} + {\vec{v}}_{2}) = c \cdot f ({\vec{v}}_{1}) + f ({\vec{v}}_{2})$

대표적인 선형 함수가 공변벡터이다. 내적의 성질

$\underset{―}{w} \cdot ({\vec{v}}_{1} + {\vec{v}}_{2}) = \underset{―}{w} \cdot {\vec{v}}_{1} + \underset{―}{w} \cdot {\vec{v}}_{2}$

$\underset{―}{w} \cdot (c \vec{v}) = c \underset{―}{w} \cdot \vec{v}$

를 함수로 바꿔서 생각하면

$\underset{―}{w} ({\vec{v}}_{1} + {\vec{v}}_{2}) = \underset{―}{w} ({\vec{v}}_{2}) + \underset{―}{w} ({\vec{v}}_{2})$

$\underset{―}{w} (c \cdot \vec{v}) = c \cdot \underset{―}{w} (\vec{v})$

이므로 공변벡터는 선형 함수임을 알 수 있다.^[각주:3]

이제 1개의 벡터가 아닌 2개의 벡터를 변수로 하고 결과로 스칼라가 나오는 함수 $A$ 를 생각해보자.

$A (\vec{v_{1}}, \vec{v_{2}}) = scalar$

만약 $A$ 가 두번째 벡터를 고정했을 때, 첫번째 벡터에 대해서 선형이라고 하자.

$A (c {\vec{v}}_{1} + {\vec{v}}_{2}, \vec{w}) = c \cdot A ({\vec{v}}_{1}, \vec{w}) + A ({\vec{v}}_{2}, \vec{w})$

또한 첫번째 벡터를 고정했을 때, 두번째 벡터에 대해서도 선형이라고 하자.

$A (\vec{v}, c {\vec{w}}_{1} + {\vec{w}}_{2}) = c \cdot A (\vec{v}, {\vec{w}}_{1}) + A (\vec{v}, {\vec{w}}_{2})$

이 두 조건을 만족하는 경우 함수 $A$ 를 (0,2)-텐서라고 부른다. 즉, (0,2)-텐서는 2개의 벡터를 변수로 하고 결과로 스칼라가 나오는 함수인데 첫번째 벡터에 대해서 선형 조건을 만족하고, 두번째 벡터에 대해서도 선형 조건을 만족하는 함수이다.

변수로 2개의 벡터가 아닌, 3개의 벡터인 경우 (0,3)-텐서, 4개의 벡터인 경우 (0,4)-텐서가 된다. 일반적으로 q개의 벡터가 들어가 결과로 스칼라가 나오고, 각 벡터에 대해서 선형인 경우 (0,q)-텐서라고 부른다.

꼭 변수로 벡터만 할 필요는 없을 것이다. 2개의 공변벡터를 변수로 하고 결과로 스칼라가 나오는 함수 $C$ 를 생각해보자.

$C ({\underset{―}{w}}_{1}, {\underset{―}{w}}_{2})$

(0,2)-텐서와 마찬가지로 한쪽을 제외한 나머지를 고정했을 때, 선형이 되는 경우 함수 $C$ 를 (2,0)-텐서라고 부른다.

$C (c {\underset{―}{w}}_{1} + {\underset{―}{w}}_{2}, \underset{―}{v}) = c \cdot C ({\underset{―}{w}}_{1}, \underset{―}{v}) + C ({\underset{―}{w}}_{2}, \underset{―}{v})$

$C (\underset{―}{w}, c {\underset{―}{v}}_{1} + {\underset{―}{v}}_{2}) = c \cdot C (\underset{―}{w}, {\underset{―}{v}}_{1}) + C (\underset{―}{w}, {\underset{―}{v}}_{2})$

3개의 공변벡터를 변수로 하는 경우 (3,0)-텐서, 4개의 공변벡터인 경우 (4,0)-텐서가 된다. 일반적으로 p개의 공변벡터가 들어가고 결과로 스칼라가 나오고, 각 공변벡터에 대해서 선형인 경우 (p,0)-텐서라고 부른다.

꼭 변수로 한 종류의 벡터만 들어갈 필요는 없다. 만약 2개의 공변벡터, 1개의 벡터를 변수로 하고, 각각에 대해서 선형인 경우 (2,1)-텐서라고 부른다.

이를 일반화하면, p개의 공변벡터, q개의 벡터를 변수로 하여 결과로 스칼라가 나오고, 각각에 대해서 선형인 경우 (p,q)-텐서라고 부른다.

기억해야 할 것은 텐서는 ① 벡터나 공변벡터가 들어가는 함수라는 것 ② 결과로 스칼라가 나온다는 것 ③ 각각의 투입에 대해서 선형 함수라는 것 ④ p개의 공변벡터, q개의 벡터가 들어가는 경우 (p,q)-텐서라고 부른다는 것이다.

#(0,2)-텐서의 세부 구조

그렇다면 텐서의 실제 연산은 어떻게 이루어지는 것일까? 한마디로 정리하면, 텐서는 여러개의 내적들을 독립적으로 수행한다음 그 결과를 곱하는 것으로 이해할 수 있다. (0,2)-텐서부터 자세히 살펴보자.

(0,2)-텐서 $A$ 안에는 첫번째 벡터와 연산이 되는 공변벡터 ${\underset{―}{W}}_{1}$ 과 두번째 벡터와 연산이 되는 공변벡터 ${\underset{―}{W}}_{2}$ 가 존재한다. 변수 $({\vec{v}}_{1}, {\vec{v}}_{2})$ 가 들어오면 각각 ${\underset{―}{W}}_{1}$ 과 ${\underset{―}{W}}_{2}$ 에 들어가 결과로 스칼라가 나오게 된다. 각각 나온 스칼라를 곱해주면 최종적인 결과값인 스칼라가 나오게 된다. $A$ 안에 벡터 2개가 들어오면 첫번째 벡터는 ${\underset{―}{W}}_{1}$ 과 두번째 벡터는 ${\underset{―}{W}}_{2}$ 와 연산이 된다는 것을 다음과 같이 표기한다.

NOTATION (0,2)-텐서

$A = {\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}$

그리고 ${\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}$ 에 ${\vec{v}}_{1}$ 과 ${\vec{v}}_{2}$ 가 들어왔을 때 연산을 다음과 같이 한다.

NOTATION (0,2)-텐서 계산

$[{\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}] ({\vec{v}}_{1}, {\vec{v}}_{2}) = {\underset{―}{W}}_{1} ({\vec{v}}_{1}) \times {\underset{―}{W}}_{2} ({\vec{v}}_{2})$

${\underset{―}{W}}_{1} ({\vec{v}}_{1})$ 과 ${\underset{―}{W}}_{2} ({\vec{v}}_{2})$ 는 각각 내적이므로 결과가 스칼라임을 기억하자. 따라서 이 둘의 곱 역시 스칼라가 된다. 실제로 이 연산이 첫번째 벡터에 대해서 선형이 되는지 확인해보자. 두번째 벡터를 $\vec{v}$ 로 고정했을 때,

$\begin{aligned} [{\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}] (c \vec{a} + \vec{b}, \vec{v}) & = {\underset{―}{W}}_{1} (c \vec{a} + \vec{b}) \times {\underset{―}{W}}_{2} (\vec{v}) \\ = {c \cdot {\underset{―}{W}}_{1} (\vec{a}) + {\underset{―}{W}}_{1} (\vec{b})} \times {\underset{―}{W}}_{2} (\vec{v}) \\ = c \cdot {{\underset{―}{W}}_{1} (\vec{a}) \times {\underset{―}{W}}_{2} (\vec{v})} + {{\underset{―}{W}}_{1} (\vec{b}) \times {\underset{―}{W}}_{2} (\vec{v})} \\ = c [{\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}] (\vec{a}) + [{\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}] (\vec{b}) \end{aligned}$

첫번째 벡터를 고정했을 때, 두번째 벡터에 대해서 선형이 되는 것도 같은 방식으로 확인할 수 있다.

만약 투입되는 벡터의 순서를 바꾸면 어떻게 될까?

$[{\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}] ({\vec{v}}_{2}, {\vec{v}}_{1})$

는 ${\underset{―}{W}}_{1}$ 과 ${\vec{v}}_{2}$ , ${\underset{―}{W}}_{2}$ 와 ${\vec{v}}_{1}$ 이 각각 연산이 되므로, 당연히 최종 결과값은 일반적으로 같지 않다는 것을 알 수 있다.

$[{\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}] ({\vec{v}}_{1}, {\vec{v}}_{2}) \neq [{\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}] ({\vec{v}}_{2}, {\vec{v}}_{1})$

만약 대응되는 공변벡터의 순서가 바뀌면 어떻게 될까? 당연히 같은 투입에 대해서 다른 결과값이 나오므로, 서로 다른 텐서라는 것을 알 수 있다.

${\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2} \neq {\underset{―}{W}}_{2} \otimes {\underset{―}{W}}_{1}$

상대성이론에서는 텐서를 성분으로 표현하는 경우가 많다. $A$ 안에 첫번째 공변벡터 ${\underset{―}{W}}_{1}$ , 두번째 공변벡터 ${\underset{―}{W}}_{2}$ 가 들어있다는 것을 성분으로는 다음과 같이 표현한다.

NOTATION (0,2)-텐서의 성분 표현

$A = {\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2} ⟶ A_{i j} = (W_{1})_{i} (W_{2})_{j}$

$A_{i j}$ 의 밑에 인덱스가 2개 있는 것은 텐서 $A$ 안에 공변벡터가 2개 들어있다는 뜻이다. (2,0)-텐서나 (2,1)-텐서에서 보겠지만, 벡터가 들어있는 경우에는 위쪽에 인덱스가 붙게 된다. 첫번째 인덱스 $i$ 는 함수 입장에서는 첫번째 벡터 투입구가 된다. 두번째 인덱스 $j$ 는 두번째 벡터 투입구이다. 우변의 $(W_{1})_{i}$ 는 i 인덱스 투입구가 $W_{1}$ 과 연산이 된다는 것을 표현한다. 똑같이 $(W_{2})_{j}$ 는 j 인덱스 투입구가 $W_{2}$ 와 연산이 된다는 것을 표현한다.

NOTATION (0,2)-텐서 계산의 성분 표현

$\begin{matrix} A ({\vec{v}}_{1}, {\vec{v}}_{2}) = [{\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}] ({\vec{v}}_{1}, {\vec{v}}_{2}) = {\underset{―}{W}}_{1} ({\vec{v}}_{1}) \times {\underset{―}{W}}_{2} ({\vec{v}}_{2}) \\ ⟶ A_{i j} (v_{1})^{i} (v_{2})^{j} = (W_{1})_{i} (W_{2})_{j} (v_{1})^{i} (v_{2})^{j} = (W_{1})_{i} (v_{1})^{i} (W_{2})_{j} (v_{2})^{j} \end{matrix}$

성분 표현의 $(v_{1})^{i}$ 는 $v_{1}$ 이 i 인덱스에 투입된다는 뜻이다. $A_{i j}$ 에서 i 인덱스는 첫번째 벡터 투입구이므로, $A$ 안에서 첫번째 공변벡터와 내적된다는 뜻이 된다. 똑같이 $(v_{2})^{j}$ 는 $v_{2}$ 가 j 인덱스, 즉, $A$ 안의 두번째 공변벡터와 내적된다는 뜻이다. 성분 표현에서 $A_{i j}$ , $(v_{1})^{i}$ , $(W_{2})_{j}$ 와 같은 것들은 숫자처럼 취급되어 위치가 중요하지 않게 된다. 즉,

$A_{i j} (v_{1})^{i} (v_{2})^{j} = (v_{1})^{i} A_{i j} (v_{2})^{j} = (v_{1})^{i} (v_{2})^{j} A_{i j} = \dots$

성분 표현에서 중요한 것은 위쪽과 아래쪽의 인덱스에서 겹치는 인덱스이다. 위쪽의 i 인덱스는 $A$ 의 i 인덱스에, 위쪽의 j 인덱스는 $A$ 의 j 인덱스에 투입된다는 것만 의미가 있다. 성분표현에서 위쪽과 아래쪽에 겹치는 인덱스는 $\sum$ 이 생략되어 있다는 것을 주의! 즉, $A_{i j} (v_{1})^{i} (v_{2})^{j}$ 는 사실은

$\sum_{i} \sum_{j} A_{i j} (v_{1})^{i} (v_{2})^{j}$

를 표현한다.

(0,2)-텐서와 마찬가지로, (0,3)-텐서, (0,4)-텐서 등도 모두 이해할 수 있다. 일반적으로 (0,q)-텐서는 안에 각 투입되는 q개의 벡터와 연산이 되는 공변벡터가 q개 존재한다. 각각의 투입과 내적하고 그 결과를 모두 곱하여 최종 함수값을 내놓는다.

이를 수식으로 다음과 같이 표기한다.

NOTATION (0,q)-텐서와 연산

위 그림과 같이, ${\vec{v}}_{1}$ 에 ${\underset{―}{W}}_{1}$ , ${\vec{v}}_{2}$ 에 ${\underset{―}{W}}_{2}$ , ... 와 같이 연산되는 (0,q)-텐서 $B$ 를 다음과 같이 표기한다.

$B = {\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2} \otimes \dots \otimes {\underset{―}{W}}_{q}$

그리고 (0,q)-텐서의 함수값은 다음과 같이 계산한다.

$B ({\vec{v}}_{1}, {\vec{v}}_{2}, \dots, {\vec{v}}_{q}) = [{\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2} \otimes \dots \otimes {\underset{―}{W}}_{q}] ({\vec{v}}_{1}, {\vec{v}}_{2}, \dots, {\vec{v}}_{q}) = {\underset{―}{W}}_{1} ({\vec{v}}_{1}) \times {\underset{―}{W}}_{1} ({\vec{v}}_{1}) \times \dots \times {\underset{―}{W}}_{q} ({\vec{v}}_{q})$

이 연산을 벡터의 성분을 이용하여 표기할 수 있다. 위에서 벡터의 성분을 이용한 표기법

${\underset{―}{W}}_{1} ({\vec{v}}_{1}) ⟶ (W_{1})_{i} (v_{1})^{i}$

와 같이 표현한 것을 그대로 이용하면,

NOTATION (0,q)-텐서의 성분 표현

$\begin{matrix} {\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2} \otimes \dots \otimes {\underset{―}{W}}_{q} = B & ⟶ & (W_{1})_{j_{1}} (W_{2})_{j_{2}} \dots (W_{q})_{j_{q}} = B_{j_{1}, j_{2}, \dots, j_{q}} \\ B ({\vec{v}}_{1}, {\vec{v}}_{2}, \dots, {\vec{v}}_{q}) & ⟶ & B_{j_{1}, j_{2}, \dots, j_{q}} (v_{1})^{j_{1}} (v_{2})^{j_{2}} \dots (v_{q})^{j_{q}} \end{matrix}$

(복잡하지만 인덱스를 잘 구별하자. 1,2,3,...q는 투입되는 순서의 인덱스이고, $j_{1}$ , $j_{2}$ , ... $j_{q}$ 는 각 벡터의 성분의 인덱스이다. 서로 내적이 되는 벡터와 공변벡터는 인덱스가 똑같음을 확인할 것. 위쪽과 아래쪽에서 똑같은 인덱스가 있다는 것은 $\sum_{(겹치는 인덱스)}$ 이 생략되어 있음을 기억할 것.)

#(2,0)-텐서의 세부 구조

같은 방식으로 (2,0)-텐서의 구조도 생각해볼 수 있다. (0,2)-텐서와 바뀐게 있다면, 투입되는 것이 공변벡터이므로 텐서 내부에는 공변벡터 대신 벡터가 있어야 한다는 점이다.

그림과 같이 $C$ 안에 첫번째 공변벡터와 연산이 되는 벡터를 ${\vec{V}}_{1}$ , 두번째 공변벡터와 연산이 되는 벡터를 ${\vec{V}}_{2}$ 가 존재한다. (0,2)-텐서와 같이 이 구조와 함수값 계산을 다음과 같이 표기할 수 있다.

NOTATION (2,0)-텐서

$C = {\vec{V}}_{1} \otimes {\vec{V}}_{2}$

$[{\vec{V}}_{1} \otimes {\vec{V}}_{2}] ({\underset{―}{w}}_{1}, {\underset{―}{w}}_{2}) = {\vec{V}}_{1} ({\underset{―}{w}}_{1}) \times {\vec{V}}_{2} ({\underset{―}{w}}_{2})$

다시 한번, ${\vec{V}}_{1} ({\underset{―}{w}}_{1})$ 과 ${\vec{V}}_{2} ({\underset{―}{w}}_{2})$ 는 내적연산으로 결과가 스칼라가 된다는 것을 강조한다. 이 연산을 성분으로 표현하면 다음과 같이 표기된다.

NOTATION (2,0)-텐서의 성분 표현

$\begin{matrix} {\vec{V}}_{1} \otimes \vec{V_{2}} = C & ⟶ & (V_{1})^{i_{1}} (V_{2})^{i_{2}} = C^{i_{1}, i_{2}} \\ C ({\underset{―}{w}}_{1}, {\underset{―}{w}}_{2}) & ⟶ & C^{i_{1}, i_{2}} ({\underset{―}{w}}_{1})_{i_{1}} ({\underset{―}{w}}_{2})_{i_{2}} \end{matrix}$

같은 방식으로 (p,0)-텐서의 구조도 생각할 수 있다. 아래 그림을 보고 직접 (p,0)-텐서를 어떻게 써야할지 생각해 보도록 하자.

#(p,q)-텐서의 세부 구조

그렇다면, (2,1)-텐서의 기본 구조 역시 생각해 볼 수 있을 것이다.

(2,1)-텐서 $E$ 에는 각각 투입에 대응하는 벡터 ${\vec{V}}_{1}$ , ${\vec{V}}_{2}$ , 공변벡터 $\underset{―}{W}$ 이 존재한다. 위에서 본 것과 마찬가지로 이 구조를 다음과 같이 표기한다.

DEFINITION (2,1)-텐서, 연산, 성분표현

$\begin{matrix} E = {\vec{V}}_{1} \otimes {\vec{V}}_{2} \otimes \underset{―}{W} & ⟶ & E_{j}^{i_{1}, i_{2}} = (V_{1})^{i_{1}} (V_{2})^{i_{2}} (W)_{j} \\ E ({\underset{―}{w}}_{1}, {\underset{―}{w}}_{2}, \vec{v}) & ⟶ & E_{j}^{i_{1}, i_{2}} (w_{1})_{i_{1}} (w_{2})_{i_{2}} v^{j} \end{matrix}$

성분표현에서 인덱스를 잘 보면, 벡터에 해당하는 인덱스는 위에 쓰고, 공변벡터에 해당하는 인덱스는 아래에 쓴다. 따라서 $E_{j}^{i_{1}, i_{2}}$ 는 위에 인덱스가 2개, 아래에 인덱스가 1개 있으므로, 텐서 $E$ 안에는 벡터가 2개, 공변벡터가 1개 있음을 알 수 있다. 이로부터 $E$ 는 투입에 공변벡터 2개, 벡터가 1개가 필요함을 역으로 추론할 수도 있다.

(p,q)-텐서의 기본 구조도 다음 그림으로부터 유추할 수 있다. 스스로 정리해볼것.

#Pure tensor가 아닌 경우

지금까지 살펴본 텐서는 pure tensor라는 종류의 텐서들이다. 더 일반적인 텐서들은 이 pure tensor들의 합으로 이루어져 있다. 즉, 같은 (p,q)-텐서 종류의 합, 빼기, 스칼라 곱은 (p,q)-텐서가 된다. 예를 들어 $A$ 와 $B$ 가 둘다 (2,1)-텐서이면, $T = c A + B$ 도 (2,1)-텐서가 된다. $A$ 와 $B$ 가 함수이므로 함수의 덧셈, 함수의 스칼라 곱으로 해석하면 된다. 즉

$T ({\underset{―}{w}}_{1}, {\underset{―}{w}}_{2}, \vec{v}) = c \cdot A ({\underset{―}{w}}_{1}, {\underset{―}{w}}_{2}, \vec{v}) + B ({\underset{―}{w}}_{1}, {\underset{―}{w}}_{2}, \vec{v})$

로 계산할 수 있다. 이를 그림으로 표현하자면 다음과 같다.

따라서 텐서끼리의 덧셈, 뺄셈, 스칼라 곱 연산을 표현할 수 있다. 함수로 생각했을 때는 특별한 내용은 없다. 다만 물리학과에서는 성분 표현을 많이 사용하므로 성분 표현만 살펴본다.

NOTATION 텐서의 덧셈, 뺄셈, 스칼라 곱의 성분 표현

(p,q)-텐서 $A$ 와 $B$ , 스칼라 $c$ 에 대하여 텐서의 덧셈, 뺄셈, 스칼라 곱을 성분으로 표현하면 다음과 같다.

$\begin{matrix} S = A + B & ⟶ & S_{j_{1}, j_{2}, \dots, j_{q}}^{i_{1}, i_{2}, \dots, i_{p}} = A_{j_{1}, j_{2}, \dots, j_{q}}^{i_{1}, i_{2}, \dots, i_{p}} + B_{j_{1}, j_{2}, \dots, j_{q}}^{i_{1}, i_{2}, \dots, i_{p}} \\ T = A - B & ⟶ & T_{j_{1}, j_{2}, \dots, j_{q}}^{i_{1}, i_{2}, \dots, i_{p}} = A_{j_{1}, j_{2}, \dots, j_{q}}^{i_{1}, i_{2}, \dots, i_{p}} - B_{j_{1}, j_{2}, \dots, j_{q}}^{i_{1}, i_{2}, \dots, i_{p}} \\ U = c A & ⟶ & U_{j_{1}, j_{2}, \dots, j_{q}}^{i_{1}, i_{2}, \dots, i_{p}} = c A_{j_{1}, j_{2}, \dots, j_{q}}^{i_{1}, i_{2}, \dots, i_{p}} \end{matrix}$

덧셈, 뺄셈에서는 $A$ 와 $B$ 의 위쪽 인덱스끼리 완전히 같아야 한다. 마찬가지로 아래쪽 인덱스끼리도 완전히 같아야 한다. 내적(위쪽 인덱스와 아래쪽 인덱스가 하나씩 짝지어지는 것)과는 다르니 헷갈리지 않도록 하자.

다시 한번, 인덱스가 복잡해 보이지만 벡터에 해당하는 인덱스는 위에 쓰고, 공변벡터에 해당하는 인덱스는 아래에 쓴다는 것을 기억하면, 각 텐서들이 위에 인덱스가 p개, 아래에 인덱스가 q개 있으므로, 안에는 벡터가 p개, 공변벡터가 q개 있음을 알 수 있다.

#Contraction

만약 (0,2)-텐서에 첫번째 벡터를 넣고, 두번째 벡터에는 아무것도 넣지 않으면 어떤 일이 일어날까? 다음 그림을 살펴보자.

$A$ 안에 들어있는 첫번째 공변벡터는 투입된 첫번째 벡터와 연산이 되어 스칼라가 될 것이다. 그러나 두번째 공변벡터는 투입된 벡터가 없기 때문에 그냥 공변벡터로 남아있을 것이다. 따라서 결과들을 곱하려 하면, (스칼라)×(공변벡터) 이므로 결과는 공변벡터가 나온다.

조금더 정확히 계산을 해보자. $A = {\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}$ 인 경우, 첫번째 투입 벡터가 $\vec{v}$ 라면, 첫번째 연산은 스칼라 ${\underset{―}{W}}_{1} (\vec{v})$ 이므로 남은 공변벡터 ${\underset{―}{W}}_{2}$ 에 곱해져, 최종 함수값은 ${\underset{―}{W}}_{1} (\vec{v}) {\underset{―}{W}}_{2}$ 가 된다. 이를 수학적으로 다음과 같이 표기한다.

Notation

(0,2)-텐서 $A$ 에 대하여, 첫번째 벡터 $\vec{v}$ 만 투입되고 두번째 벡터는 투입되지 않는 것을 다음과 같이 표기한다.

$A (\vec{v}, \cdot)$

만약 $A = {\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}$ 인 경우 위 수식은 다음과 같이 계산한다.

$[{\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}] (\vec{v}, \cdot) = {\underset{―}{W}}_{1} (\vec{v}) \underset{―}{W_{2}}$

이를 성분으로 표현하면 다음과 같이 된다.

$\begin{matrix} A (\vec{v}, \cdot) & ⟶ & A_{j_{1}, j_{2}} v^{j_{1}} \\ [{\underset{―}{W}}_{1} \otimes {\underset{―}{W}}_{2}] (\vec{v}, \cdot) = {\underset{―}{W}}_{1} (\vec{v}) {\underset{―}{W}}_{2} & ⟶ & [(W_{1})_{j_{1}} (W_{2})_{j_{2}}] v^{j_{1}} = (W_{1})_{j_{1}} v^{j_{1}} (W_{2})_{j_{2}} \end{matrix}$

이렇게 모두 함수의 투입구에 모두 투입하지 않고 일부만 투입하는 연산을 contraction이라고 한다. 꼭 첫번째 투입구에 넣을 필요는 없다. 첫번째는 비워두고 두번째 벡터만 넣는 경우도 생각할 수 있을 것이다.

이러한 경우 함수의 표현으로는

$A (\cdot, \vec{v})$

성분 표현으로는

$A_{j_{1}, j_{2}} v^{j_{2}}$

가 된다. 여기서 특별히 주의를 기울여야 하는 것은 성분 표현이다. 위에서 첫번째 투입구에 벡터를 넣은 것과 비교해보자. $v$ 의 인덱스를 잘 살펴보면, 첫번째 투입구에 넣은 경우에는 $A$ 의 첫번째 아래 인덱스와 똑같다는 것을 알 수 있다. 두번째 투입구에 넣은 경우에는 $A$ 의 두번째 아래 인덱스와 똑같다. 이런 식으로 성분 표현에서는 어떤 인덱스끼리 똑같냐에 따라 어떤 투입구에 넣었냐가 결정된다.

이제, 이 그림의 경우 쉽게 이해할 수 있을 것이다. 이를 식으로 쓰면

$C (\underset{―}{w}, \cdot)$

또는

$C^{i_{1}, i_{2}} w_{i_{1}}$

으로 쓸 수 있다.

이 그림의 경우는 contraction의 의미를 확실하게 알 수 있다. (2,1)-텐서에 일부만 투입을 하면, (1,1)-텐서로 축소(contraction) 되는 것을 볼 수 있다. 특히 함수 표현 $E (\cdot, \underset{―}{w}, \cdot) = T$ 를 성분 표현으로 쓰면

$E_{j}^{i_{1}, i_{2}} w_{i_{2}} = T_{j}^{i_{1}}$

로 결과 텐서 $T$ 가 위쪽 인덱스 1개, 아래쪽 인덱스 1개로 (1,1)-텐서가 됨을 알 수 있다. 마치 $E$ 의 위쪽 인덱스 $i_{2}$ 와 $w$ 의 아래쪽 인덱스 $i_{2}$ 가 약분되서 없어지는 효과처럼 생각할 수 있다. 다만 실제 계산 값은 반드시 위 그림을 따라서 계산해야 한다.

가장 복잡한 경우는 텐서와 텐서의 contraction이다. 일단 그림으로 생각해보자.

텐서와 텐서의 contraction은 먼저 텐서를 완전히 벡터와 공변벡터로 분해한다. 그리고 contraction하고자 하는 벡터와 공변벡터끼리 내적한후 남은 것들을 순서대로 배열한다. 배열 순서는 (앞에 있는 텐서의 남은 벡터), (뒤에 있는 텐서의 남은 벡터), (앞에 있는 텐서의 남은 공변벡터), (뒤에 있는 텐서의 남은 공변벡터)로 배열하자.^[각주:4] 텐서와 텐서의 contraction은 함수의 형태로 표기하기에는 적합하지 않다. 따라서 보통 성분 표현을 이용하여 표현한다. 위 그림과 같은 경우의 성분 표현은 다음과 같이 표현된다.

$A_{j}^{i_{1}, i_{2}} B_{i_{2}, i_{1}, j_{1}, j_{2}}^{j, i_{3}} = C_{j_{1}, j_{2}}^{i_{3}}$

인덱스를 잘 살펴보자. 먼저 좌변에서 위와 아래쪽 인덱스에 동시에 출현하는 인덱스들은 $i_{1}$ , $i_{2}$ , $j$ 이다. $i_{1}$ 의 위치는 $A$ 에서는 첫번째 벡터, $B$ 에서는 두번째 공변벡터 위치이다. 따라서 $A$ 와 $B$ 를 분해한 뒤, $A$ 의 첫번째 벡터와 $B$ 의 두번째 공변벡터를 내적한다는 뜻이다. $i_{2}$ 의 위치는 $A$ 에서는 두번째 벡터, $B$ 에서는 첫번째 공변벡터 위치이므로 각 위치의 벡터와 공변벡터를 내적한다. 위 식에서 $j$ 의 위치를 보고, 어떤 벡터와 공변벡터가 내적하는지 생각해보고 그림에서 확인해 보자.

꼭 contraction이 2개의 텐서에서 계산될 필요는 없다. 하나의 텐서를 분해해서 그 안에서 내적을 한다면 그 것 역시 contraction이 된다.

중요한 것은 성분 표현에서 인덱스를 contraction이 되는 것들끼리 같은 문자를 배정해야 한다는 것이다. contraction이 되지 않는 것은 서로 다른 문자를 배정해야 한다.

#텐서곱

마지막 텐서의 연산으로 텐서곱을 살펴본다. 텐서곱은 간단히 분해 후 재배열 이다. 다음 그림을 살펴보자.

텐서와 텐서를 완전히 벡터와 공변벡터로 분해하고, 다시 재배열 하는 것으로 생각할 수 있다. 배열 순서는 contraction과 같이 (앞에 있는 텐서의 벡터), (뒤에 있는 텐서의 벡터), (앞에 있는 텐서의 공변벡터), (뒤에 있는 텐서의 공변벡터)로 배열하자.^[각주:5] 이 연산을 다음과 같이 표기한다.

NOTATION 텐서곱

두 텐서 $A$ 와 $B$ 의 텐서곱을 다음과 같이 표기한다.

$A \otimes B$

텐서곱을 성분으로 표현하면 다음과 같이 표기된다.

$\begin{matrix} A \otimes B = C & ⟶ & A_{j}^{i_{1}, i_{2}} B_{l}^{k} = C_{j, l}^{i_{1}, i_{2}, k} \end{matrix}$

텐서곱은 다음과 같이 분배법칙이 성립한다.

THEOREM 텐서곱과 텐서 합의 분배법칙

$\begin{matrix} A \otimes (B + C) & = & (A \otimes B) + (A \otimes C) \\ (D + E) \otimes F & = & (D \otimes F) + (E \otimes F) \end{matrix}$

위 식의 덧셈은 덧셈 조건에 맞아야 한다. 즉, $B$ , $C$ 는 같은 (p,q)-텐서. 분배법칙을 성분으로 표현하면 다음과 같이 표기된다.

$A_{j_{1}, j_{2}, \dots, j_{β}}^{i_{1}, i_{2}, \dots, i_{α}} (B_{l_{1}, l_{2}, \dots, l_{q}}^{k_{1}, k_{2}, \dots, k_{p}} + C_{l_{1}, l_{2}, \dots, l_{q}}^{k_{1}, k_{2}, \dots, k_{p}}) = (A_{j_{1}, j_{2}, \dots, j_{β}}^{i_{1}, i_{2}, \dots, i_{α}} B_{l_{1}, l_{2}, \dots, l_{q}}^{k_{1}, k_{2}, \dots, k_{p}}) + (A_{j_{1}, j_{2}, \dots, j_{β}}^{i_{1}, i_{2}, \dots, i_{α}} C_{l_{1}, l_{2}, \dots, l_{q}}^{k_{1}, k_{2}, \dots, k_{p}})$

텐서의 덧셈, 뺄셈, 스칼라곱은 같은 쪽에서 인덱스가 같아야 함을 주의.

재해석

이번 페이지에서는 텐서의 세부 구조와 표기법, 연산에 대하여 살펴보았다. 분명 여기 내용만으로 모든것을 알 수 없을 것이다. 다만, 상대성이론이나 다른 텐서가 나오는 부분을 보면서, 여기에 나온 구조와 연산, 표기법으로 정리한다면 텐서가 계산량만 많고 식만 길뿐, 벡터 연산과 다를바 없다는 것을 금방 이해할 것이라 생각된다.

마지막으로 살펴볼 내용은 벡터를 (1,0)-텐서, 공변벡터를 (0,1)-텐서로 생각하고 이 페이지의 처음부터 끝까지를 contraction과 텐서곱으로 재해석하는 것이다. (1,0)-텐서와 (0,1)-텐서의 contraction은 선택의 여지 없이 내적일 수밖에 없다. (1,0)-텐서를 p번 텐서곱을 하면, (p,0)-텐서를 얻고, (0,1)-텐서를 q번 텐서곱을 하면, (0,q)-텐서를 얻는다. 이 둘을 다시 텐서곱을 하면 (p,q)-텐서를 얻을 수 있다. 또한, 내적이 contraction이므로 텐서와 벡터, 공변벡터 사이의 연산은 contraction으로 모두 표현된다. 결국 텐서의 연산은 덧셈, 스칼라곱, contraction, 텐서곱으로 모두 해석할 수 있다. 이러한 관점에서 다시 한번 이 페이지를 읽는다면 텐서의 연산에 대하여 더 자세히 알 수 있을 것이다.

Example

1. 코시 응력 텐서(Cauchy stress tensor)

유체역학이나 구조역학 등에서 나오는 코시 stress 텐서는 다음과 같은 행렬로 정의된다.

$σ = [\begin{matrix} σ_{x x} & σ_{x y} & σ_{x z} \\ σ_{y x} & σ_{y y} & σ_{y z} \\ σ_{z x} & σ_{z y} & σ_{z z} \end{matrix}]$

$σ_{i j}$ 는 i 방향을 normal vector로 가지는 평면^[각주:6]에 작용하는 j 방향 stress를 표현한다. 예를 들어, $σ_{y z}$ 는 normal vector가 y인 평면(즉, xz평면)에 작용하는 z방향 stress의 크기이다.

Sanpaz / CC BY-SA via Wikimedia

코시 stress 텐서의 가장 기본적인 것은 평면의 normal vector $n$ 과 $σ$ 가 연산되면 평면에 작용하는 stress 벡터 $T^{(n)}$ 를 얻는다.

$σ \cdot n = T^{(n)}$

평면의 normal vector가 공변벡터라는 사실로부터, 공변벡터와 연산되어 벡터가 나오는 텐서는 (2,0)-tensor이므로, 코시 stress 텐서는 (2,0)-tensor임을 알 수 있다. 다만 코시 stress 텐서는 pure 텐서가 아니기 때문에, 위 식을 해석하기 위하여 3가지 pure 텐서 $A$ , $B$ , $C$ 를 생각해보자.

Normal vector $n$ 이 $A$ 에 있는 첫번째 벡터인 x축 단위벡터에 들어가서 내적을 하면, 내적의 정의

$\vec{a} \cdot \vec{b} = | a | | b | \cos θ$

로부터 $n$ 과 x축 단위벡터 사이의 각도의 cosine값이 얻어진다.^[각주:7] Normal vector의 의미를 생각하면, 이 값은 동시에 $n$ 이 표현하는 평면과 yz-평면 사이의 각도 $θ_{x}$ 의 cosine값이 된다. 따라서 이 값을 두번째 벡터인 yz-평면에 작용하는 stress 벡터 $T^{(e_{x})}$ 와 곱하게 되면

$A (n, \cdot) = T^{(e_{x})} \cos θ_{x}$

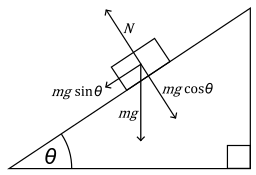
가 된다. 즉, $n$ 평면과 yz-평면 사이의 각도에 의해 stress vector값을 투영하는 것과 같다. 이 조정값이 벡터의 내적인 각도의 cosine 값이라는 것은 본질적으로 힘의 분해와 완전히 동일하다. 아래 그림에서 중력 $m g$ 를 $N$ 방향으로 투영할 때 사이 각도인 $θ$ 에 의하여 $m g \cos θ$ 가 된다는 것을 참고하자.^[각주:8]

Mets501 / CC BY-SA via Wikimedia

텐서 $B$ 와 $C$ 는 $A$ 와 완전히 똑같다. 다만 $B$ 는 xz-평면, $C$ 는 xy-평면이라는 점만 다르다.

따라서,

1. $A$ 와 $n$ 연산 = yz-평면에 작용하는 stress값 $T^{(e_{x})}$ 을 $n$ -평면으로 투영한 벡터

2. $B$ 와 $n$ 연산 = xz-평면에 작용하는 stress값 $T^{(e_{y})}$ 을 $n$ -평면으로 투영한 벡터

3. $C$ 와 $n$ 연사 = xy-평면에 작용하는 stress값 $T^{(e_{z})}$ 을 $n$ -평면으로 투영한 벡터

가 된다. 코시 stress 텐서 $σ$ 는 $A$ , $B$ , $C$ 를 더한 것과 같다.

$σ = A + B + C$

따라서 $σ (n, \cdot)$ 은

$σ (n, \cdot) = A (n, \cdot) + B (n, \cdot) + C (n, \cdot) = T^{(e_{x})} \cos θ_{x} + T^{(e_{y})} \cos θ_{y} + T^{(e_{z})} \cos θ_{z}$

임을 알 수 있다. 즉, xy, yz, xz-평면에 작용하는 stress 벡터들을 $n$ -평면으로 투영하여 더한 값이라는 것을 알 수 있다. $σ (n, \cdot)$ 를 위에서 본 성분 표현으로 쓰면

$σ^{i j} n_{i} = {(T^{(n)})}^{j}$

가 된다. 좌변에 $\sum_{i}$ 가 생략되어 있음에 주의!

만약 코시 stress 텐서와 두번째 인덱스로 contraction을 하면 어떤 정보를 얻을 수 있을까? 다음 그림을 살펴보자.

$A$ 에 두번째 인덱스에 x방향 단위벡터를 넣으면 yz-평면에 작용하는 stress 벡터와 내적하여, yz-평면에 작용하는 stress의 x성분 벡터가 나온다. 따라서 $A$ 속에 첫번째 벡터와 곱해지면

$A (\cdot, e_{x}) = [\begin{matrix} (T^{(e_{x})})^{x} \\ 0 \\ 0 \end{matrix}]$

가 된다. 같은 방식으로

$\begin{aligned} B (\cdot, e_{x}) & = [\begin{array}{c} 0 \\ (T^{(e_{y})})^{x} \\ 0 \end{array}] & , & C (\cdot, e_{x}) & = [\begin{array}{c} 0 \\ 0 \\ (T^{(e_{z})})^{x} \end{array}] \end{aligned}$

따라서 코시 stress 텐서의 두번째 인덱스와 x방향 단위벡터가 contraction되면 다음의 결과가 얻어진다.

$σ (\cdot, e_{x}) = [\begin{matrix} (T^{(e_{x})})^{x} \\ (T^{(e_{y})})^{x} \\ (T^{(e_{z})})^{x} \end{matrix}]$

텐서의 정의, 각 벡터에 대한 선형성을 이용하면, 단위 공변벡터 $m$ 에 대해서,

$\begin{aligned} σ (\cdot, m) & = [\begin{array}{c} m_{x} (T^{(e_{x})})^{x} + m_{y} (T^{(e_{x})})^{y} + m_{z} (T^{(e_{x})})^{z} \\ m_{x} (T^{(e_{y})})^{x} + m_{y} (T^{(e_{y})})^{y} + m_{z} (T^{(e_{y})})^{z} \\ m_{x} (T^{(e_{z})})^{x} + m_{y} (T^{(e_{z})})^{y} + m_{z} (T^{(e_{z})})^{z} \end{array}] \\ = [\begin{array}{c} m \cdot T^{(e_{x})} \\ m \cdot T^{(e_{y})} \\ m \cdot T^{(e_{z})} \end{array}] \\ = [\begin{array}{c} m \cdot (yz-평면에 작용하는 stress 벡터) \\ m \cdot (xz-평면에 작용하는 stress 벡터) \\ m \cdot (xz-평면에 작용하는 stress 벡터) \end{array}] \end{aligned}$

즉, 위쪽 행부터 순서대로, yz, xz, xz-평면에 작용하는 stress 벡터를 $m$ 방향으로 투영했을 때 크기를 나타낸다. 이를 성분 표현으로 쓰면

$σ^{i j} m_{j}$

코시 stress 텐서에서 많이 쓰이는 식은 $n$ -평면의 normal 방향 stress 크기 $σ_{n}$ 이다. 이는 $n$ -평면에 작용하는 stress 벡터와 normal vector $n$ 을 내적하면 된다. 따라서

$σ_{n} = T^{(n)} \cdot n = σ (n, n)$

이를 성분 표현으로 쓰면

$σ_{n} = σ^{i j} n_{i} n_{j}$

우변에 $\sum_{i, j}$ 가 생략되어 있음에 주의! 그리고 normal 방향 stress에 직각이 되는 shear stress의 크기 $τ_{n}$ 는 피타고라스 정리에 의해

$τ_{n} = \sqrt{{(T^{(n)})}^{2} - σ_{n}^{2}}$

이고

${(T^{(n)})}^{2} = \sum_{i} {(T^{(n)})}^{i} {(T^{(n)})}^{i} = \sum_{i} σ^{i j} n_{j} σ^{i k} n_{k}$

이므로

$τ_{n} = \sqrt{\sum_{i} {σ^{i j} σ^{i k} n_{j} n_{k}} - σ^{i j} n_{i} n_{j} σ^{l k} n_{l} n_{k}}$

가 된다.

2. (2,0)-텐서 또는 (0,2)-텐서 연산의 행렬 표현

(2,0)-텐서와 (0,2)-텐서는 행렬로 표현되기도 한다. 코시 stress 텐서도 다음과 같이 행렬로 표현된다.

$σ = [\begin{matrix} σ_{x x} & σ_{x y} & σ_{x z} \\ σ_{y x} & σ_{y y} & σ_{y z} \\ σ_{z x} & σ_{z y} & σ_{z z} \end{matrix}]$

그리고 normal vector도 row 행렬이나 column 행렬로 표현된다. 그래서 (2,0)-텐서 또는 (0,2)-텐서의 연산은 행렬로 표현하여 빠르게 계산하기도 한다. 예를 들어, n-평면에 작용하는 stress 계산 $σ^{i j} n_{i} = {(T^{(n)})}^{j}$ 는

$[\begin{matrix} n_{1} & n_{2} & n_{3} \end{matrix}] [\begin{matrix} σ_{x x} & σ_{x y} & σ_{x z} \\ σ_{y x} & σ_{y y} & σ_{y z} \\ σ_{z x} & σ_{z y} & σ_{z z} \end{matrix}] = [\begin{matrix} {(T^{(n)})}^{1} & {(T^{(n)})}^{2} & {(T^{(n)})}^{3} \end{matrix}]$

로 표현된다. 텐서 연산식에서 행렬 연산이 어떻게 도출되는지 살펴보자.

$σ$ 행렬과 $n$ 행렬이 곱해질 때는2가지 가능성이 있다.

① $σ$ 가 $n$ 앞에서 곱해지는 경우

② $σ$ 가 $n$ 뒤에서 곱해지는 경우.

각 경우에 대해서 하나씩 행렬 연산과 텐서 연산식을 연결시켜보자.

먼저 $σ$ 가 $n$ 앞에서 곱해지는 경우에^[각주:9], $σ$ 행렬 안에 어떤 값들이 연산되는지 살펴보자.

$\begin{array}{r} i th row \to \end{array} [\begin{matrix} ⋮ \\ σ^{i 1} & σ^{i 2} & σ^{i 3} \\ ⋮ \end{matrix}] [\begin{matrix} n_{1} \\ n_{2} \\ n_{3} \end{matrix}] = [\begin{matrix} ⋮ \end{matrix}]$

이 경우 행렬 곱셈 식은

$σ^{i 1} n_{1} + σ^{i 2} n_{2} + σ^{i 3} n_{3} = σ^{i j} n_{j}$

가 된다. 우변에 $\sum_{j}$ 가 생략되어 있음에 주의! 이 식은 $σ$ 의 두번째 인덱스와 $n$ 의 contraction이다.

같은 방식으로 $σ$ 가 $n$ 뒤에서 곱해지는 경우에는^[각주:10]

$\begin{array}{r} \begin{array}{c} j th column \\ ↓ \end{array} \\ [\begin{array}{c} n_{1} & n_{2} & n_{3} \end{array}] [\begin{array}{c} σ^{1 j} \\ \dots & σ^{2 j} & \dots \\ σ^{3 j} \end{array}] = [\begin{array}{c} \dots \end{array}] \end{array}$

이 경우 행렬 곱셈식은

$σ^{1 j} n_{1} + σ^{2 j} n_{2} + σ^{3 j} n_{3} = σ^{i j} n_{i}$

가 된다. 이 식은 $σ$ 의 첫번째 인덱스와 $n$ 의 contraction이다.

이러한 방식으로 $σ$ 의 첫번째 인덱스와 $n$ 이, 두번째 인덱스와 $m$ 이 contraction이 되는 경우도 행렬로 표현할 수 있다.

$σ^{i j} n_{i} m_{j} = \sum_{i} n_{i} (\sum_{j} σ^{i j} m_{j}) = \sum_{i} n_{i} {([σ] \times [m])}_{i}$

이므로

$σ^{i j} n_{i} m_{j} = [\begin{matrix} \dots & n_{i} & \dots \end{matrix}] [\begin{matrix} ⋮ \\ \dots & σ^{i j} & \dots \\ ⋮ \end{matrix}] [\begin{matrix} ⋮ \\ m_{j} \\ ⋮ \end{matrix}]$

여기에서 주의해야 할 것은, (2,0)-텐서나 (0,2)-텐서를 행렬로 표현할 때, 첫번째 인덱스가 행, 두번째 인덱스가 열을 나타내야 한다. 만약 첫번째 인덱스가 열, 두번째 인덱스가 행을 나타내는 경우, 위의 결과가 뒤바뀐다. 직접 생각해볼 것.

3. 계량 텐서(metric tensor)

Metric 텐서 $g$ 는 (0,2)-텐서로서, 2개의 벡터를 받아 내적값을 주는 텐서이다.

$g (\vec{v}, \vec{w}) = \vec{v} \cdot \vec{w}$

위 식을 성분 표현으로 쓰면 다음과 같이 표현된다.

$g_{i j} v^{i} w^{j} = \vec{v} \cdot \vec{w}$

$g$ 는 (0,2)-텐서이므로, 위에서 논의한 것처럼 행렬로 표현할 수 있다. $g$ 의 구체적인 형태는 다음과 같다.

$g = [\begin{matrix} {\vec{e}}^{1} \cdot {\vec{e}}_{1} & {\vec{e}}_{1} \cdot {\vec{e}}_{2} & {\vec{e}}_{1} \cdot {\vec{e}}_{3} \\ {\vec{e}}_{2} \cdot {\vec{e}}_{1} & {\vec{e}}_{2} \cdot {\vec{e}}_{2} & {\vec{e}}_{2} \cdot {\vec{e}}_{3} \\ {\vec{e}}_{3} \cdot {\vec{e}}_{1} & {\vec{e}}_{3} \cdot {\vec{e}}_{2} & {\vec{e}}_{3} \cdot {\vec{e}}_{3} \end{matrix}]$

또는 성분 표현으로

$g_{i j} = {\vec{e}}_{i} \cdot {\vec{e}}_{j}$

벡터의 내적은 $\vec{v} \cdot \vec{w} = v^{1} w^{1} + v^{2} w^{2} + v^{3} w^{3}$ 로 간단히 표현되는데 왜 metric 텐서가 필요할까? 이 식은 기저 벡터가 서로 직교하는 단위벡터인 경우에만 성립한다. 만약 서로 직교하지 않는 경우에는

$\vec{v} \cdot \vec{w} = v^{1} w^{1} {\vec{e}}_{1} \cdot {\vec{e}}_{1} + v^{1} w^{2} {\vec{e}}_{1} \cdot {\vec{e}}_{2} + v^{1} w^{3} {\vec{e}}_{1} \cdot {\vec{e}}_{3} + \dots + \dots v^{3} w^{3} {\vec{e}}_{3} \cdot {\vec{e}}_{3}$

로 계산하여야 한다. 우변을 metric 텐서를 이용하면 간단히

$g_{i j} v^{i} w^{j}$

로 표현된다.^[각주:11]

4. 인덱스 raising과 lowering

Metric 텐서의 첫번째 인덱스와 벡터 $\vec{v}$ 의 contraction $g_{i j} v^{i}$ 를 생각해보자. 먼저 (0,2)-텐서와 (1,0)-텐서^[각주:12]의 contraction이므로 이 연산의 결과는 (0,1)-텐서, 즉 공변벡터임을 알 수 있다. 이를 $\underset{―}{a}$ 라고 하자. $\underset{―}{a}$ 와 임의의 벡터 $\vec{w}$ 의 contraction을 생각해보면,

${\underset{―}{a}}_{j} w^{j} = (g_{i j} v^{i}) w^{j} = \vec{v} \cdot \vec{w}$

즉, $\vec{v}$ 와 $\vec{w}$ 가 된다. 공변벡터와 벡터의 contraction이 본질적으로 내적이라고 한다면, $\underset{―}{a}$ 는 내적의 관점에서 $\vec{v}$ 역할을 하는 공변벡터라고 할 수 있다. 그래서 $\underset{―}{a}$ 를 $\vec{v}$ 와 같은 문자를 써서 $\underset{―}{v}$ 로 쓰는 것이 관례이다.

$g (\vec{v}, \cdot) = \underset{―}{v}$

$\vec{v}$ 는 벡터, $\underset{―}{v}$ 는 공변벡터로 분명히 다른 오브젝트이다. 다만 내적 관점에서 똑같은 연산이 된다는 뜻으로 같은 문자를 쓰는 것이다. 성분 표현으로 쓰면 다음과 같다.

$g_{i j} v^{i} = v_{j}$

Metric 텐서와의 contraction은 마치 $v$ 의 인덱스를 위에서 아래로 내리는 연산처럼 보인다. 이를 인덱스 lowering이라고 부른다.

반대로 $g$ 의 역행렬을 (2,0)-텐서 $g^{i j}$ 로 정의한다. 똑같은 방식으로 다음과 같은 연산이 정의된다.

$g^{i j} w_{i} = w^{j}$

다시한번 $w^{j}$ 는 내적 관점에서 공변벡터 $w_{j}$ 와 같은 역할을 하는 벡터이기 때문에 같은 문자를 쓴다. Metric 텐서의 역행렬과의 contraction은 마치 $w$ 의 인덱스를 아래에서 위로 올리는 연산처럼 보인다. 이를 인덱스 raising이라고 부른다.

5. 대칭 텐서(symmetric tensor)와 반대칭 텐서(antisymmetric tensor)

Metric 텐서는 정의상 첫번째 벡터와 두번째 벡터를 바꿔서 넣어도 결과가 똑같다.

$g (\vec{v}, \vec{w}) = \vec{v} \cdot \vec{w} = \vec{w} \cdot \vec{v} = g (\vec{w}, \vec{v})$

일반적인 텐서는 성립하지 않는 이러한 성질을 가진 텐서를 대칭 텐서라고 부른다. 위 식을 성분으로 표현하면

$g_{i j} v^{i} w^{j} = g_{i j} w^{i} v^{j}$

우변의 인덱스를 조금 정리하면

$g_{i j} v^{i} w^{j} = g_{j i} v^{i} w^{j}$

따라서 대칭 텐서는 성분으로 표현할 때 인덱스의 순서를 바꿔도 같은 값을 갖는다.

$g_{i j} = g_{j i}$

역으로 위 식이 성립하는 경우에 대칭 텐서가 된다.

DEFINITION 대칭 텐서

(0,2)-텐서 $S$ 가 다음을 항상 만족하는 경우 대칭 텐서라고 부른다.

$S (\vec{v}, \vec{w}) = S (\vec{w}, \vec{v})$

마찬가지로 (2,0)-텐서, (1,1)-텐서의 경우 같은 방식으로 대칭 텐서를 정의할 수 있다. 또한 대칭 텐서의 필요충분 조건은 다음과 같다.

$S_{i j} = S_{j i}$

위에서 살펴본, 코시 stress 텐서 역시 대칭 텐서이다.^[각주:13]

어떤 종류의 텐서는 첫번째 벡터와 두번째 벡터를 바꿔서 넣는 경우 결과의 부호가 반대가 된다.

$A (\vec{v}, \vec{w}) = - A (\vec{w}, \vec{v})$

이러한 성질을 가진 텐서를 반대칭 텐서라고 부른다.

DEFINITION 반대칭 텐서

(0,2)-텐서 $A$ 가 다음을 항상 만족하는 경우 반대칭 텐서라고 부른다.

$A (\vec{v}, \vec{w}) = - A (\vec{w}, \vec{v})$

마찬가지로 (2,0)-텐서, (1,1)-텐서의 경우 같은 방식으로 반대칭 텐서를 정의할 수 있다. 또한 반대칭 텐서의 필요충분 조건은 다음과 같다.

$A_{i j} = - A_{j i}$

같은 방식으로 더 일반적인 텐서에 대해서도 대칭, 반대칭을 정의할 수 있다.

6. 텐서 필드(tensor field)

지금까지 텐서에 대해서 살펴보았다. 그러나 유체역학이나 상대성이론 식에서 나오는 텐서는 사실 텐서 필드이다. 벡터장이 모든 좌표에 벡터가 붙어있는 모습인 것처럼, 텐서 필드는 모든 좌표에 텐서가 붙어있는 모습이다. 이렇게 정의된 텐서 필드에 대하여 공변 미분 등이 정의된다.

인덱스 문자 i, j는 마음대로 선택하면 된다. [본문으로]
이렇게 시그마를 생략하는 표기법을 Einstein summation convention(아인슈타인 합 규약)이라고 한다. [본문으로]
사실은 공변벡터의 정의가 벡터를 변수로 하는 선형 함수이다. 그러나 물리학과 학생들에게는 반대로 접근하는 것이 더 익숙할 것이다. [본문으로]
가장 일반적으로는 배열 순서는 텐서 식을 세우는 사람이 마음대로 정하면 된다. 다만 여기에서는 쉬운 이해를 위해 이렇게 고정한다. [본문으로]
contraction과 마찬가지로 재배열 순서는 텐서식을 세우는 사람 마음대로 정하면 된다. 여기에서는 쉬운 이해를 위해 이렇게 정렬한다. [본문으로]
normal vector가 x방향이라면 yz평면, y방향이라면 xz평면, z방향이라면 xy평면이다. --normal vector-- 참고. [본문으로]
normal vector와 단위벡터는 정의상 길이가 1. [본문으로]
$N$ 의 직각방향은 사이 각도가 $\frac{\pi}{2} - \theta$ 이므로 $\cos{\left(\frac{\pi}{2} - \theta\right)} = \sin{\theta}\$ 이므로 결국은 똑같이 사이 각도의 cosine인건 똑같다. [본문으로]
$\sigma$ 가 3x3 행렬이므로 뒤에 나올 $n$ 행렬은 3x1 행렬이 되어야 할 것이다. $n$ 행렬이 1x3 행렬인 경우에는 행렬 곱셈을 할 수 없다. [본문으로]
이 경우에는 $n$ 행렬이 1x3 행렬이 되어야 행렬 곱셈이 성립한다. [본문으로]
표현 방법은 간단하더라도 계산 과정은 생략된 $\sum _{i,j}$ 때문에 결국 똑같다. 그나마 계산 과정을 줄이는 것은 행렬을 이용하는 것이다. [본문으로]
벡터는 ① 공변벡터 1개와 연산하여 스칼라가 된다는 점 ② 내적 연산이 각각에 대해 선형이라는 점으로부터 (1,0)-텐서로 생각할 수 있다. [본문으로]
코시 stress 텐서의 대칭은 물리학의 각운동량 보존 법칙과 stress의 정의로부터 얻어진다. [본문으로]

저작자표시 비영리 동일조건

'임시페이지' 카테고리의 다른 글

Reporducing Kernel Hilbert Space (RKHS) (0)	2022.08.30
Algebra: Chapter 0, Aluffi, Exercise III.1.4 (0)	2022.01.05
Algebra: Chapter 0, Aluffi, Exercise III.1.3 (0)	2022.01.04
Algebra: Chapter 0, Aluffi, Exercise III.1.2 (0)	2022.01.04
Algebra: Chapter 0, Aluffi, Exercise III.1.1 (0)	2022.01.04
함수의 극한, $ϵ$ - $δ$ 정의 이해 (0)	2021.01.21

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

피그티의 기초물리

텐서란 무엇인가? 텐서의 이해, 표기법, 연산 완전 정리

#벡터와 공변벡터의 기본 연산

#선형 함수와 텐서

#(0,2)-텐서의 세부 구조

#(2,0)-텐서의 세부 구조

#(p,q)-텐서의 세부 구조

#Pure tensor가 아닌 경우

#Contraction

#텐서곱

재해석

Example

'임시페이지' 카테고리의 다른 글

티스토리툴바

개인정보

단축키

내 블로그

블로그 게시글

모든 영역