*이 페이지는 아직 추후 현대대수 페이지에 맞춰서 수정될 임시 페이지입니다.
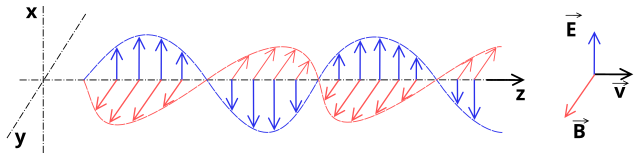
물리적으로 빛은 Maxwell’s equation에 의해 설명되는 electromagnetic field이다. 가장 이해하기 쉬운 형태는 전기장과 자기장이 서로 교차하는 plane wave로 다음과 같은 식과 그림으로 표현된다.
$$ E (x,t) = E_z \sin{\left(kx - \omega t \right)} $$
By SuperManu (Self, based on Image:Onde electromagnetique.png)
[GFDL, CC-BY-SA-3.0 or CC BY-SA 2.5 ], via Wikimedia Commons
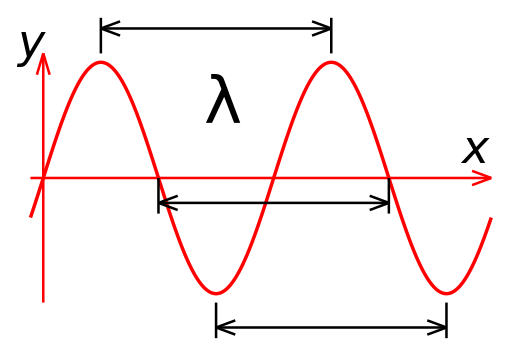
위의 식에서 electric field 크기가 최대가 되는 위치에서 최대가 되는 다음 위치까지의 거리
$$ \lambda = \frac{2 \pi}{\left| k \right|} $$
를 wavelength라고 정의한다.
By Dicklyon (Richard F. Lyon) [CC BY-SA 3.0 ], from Wikimedia Commons
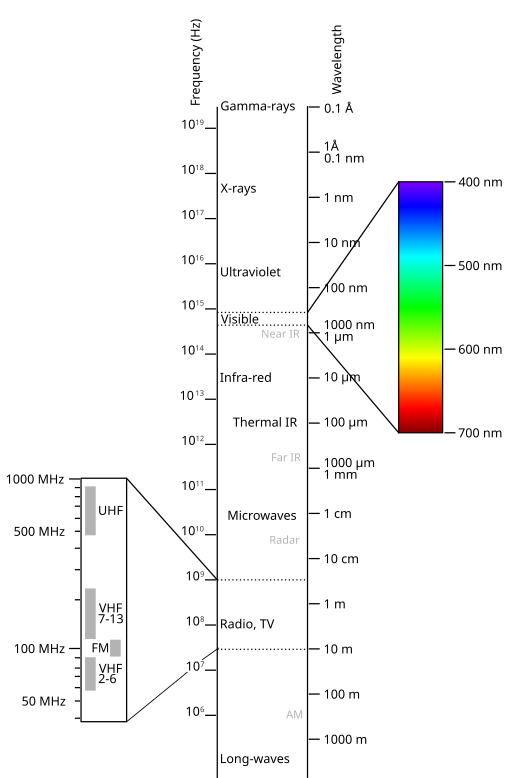
만약 wavelength가 380~800nm인 경우 그 빛을 visible light라고 부르며 빛의 color는 wavelength로 결정된다. 예를 들어 wavelength가 450nm인 빛은 파란색, 680nm인 빛은 빨간색으로 보인다.
By Original: PenubagVector:Victor Blacus (Own work based on: Electromagnetic-Spectrum.png)
[CC BY-SA 3.0 ], via Wikimedia Commons
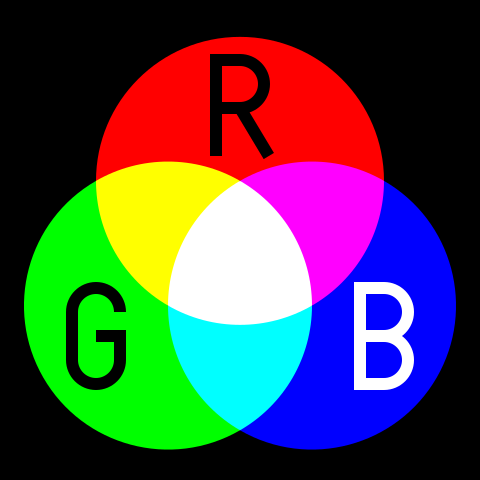
이제 색이론에서 기초가 되는 빛의 3원색을 생각해보자.
By SharkD at English WikipediaLater versions were uploaded by Jacobolus at en.wikipedia.
(Transferred from en.wikipedia to Commons.) [Public domain], via Wikimedia Commons
빛은 흔히 additive color라고 불리는데 색을 섞을수록 점점 밝아지기 때문에 그렇게 불린다. 위의 그림에서 보는 것처럼 순수한 파란색의 빛과 순수한 빨간색의 빛을 섞으면 분홍색(magenta)의 빛이 된다.
하지만 plane wave 관점에서 생각했을 때, 450nm의 파란색 plane wave와 680nm의 초록색 plane wave를 섞는 것은 단순한 wave addition이지 500nm의 aqua 색상의 plane wave가 되는 것은 아니다. 수학적으로 450nm의 plane wave와 680nm의 plane wave
$$ E_{\mathrm{blue}} = E_z \cos{\left(\frac{2\pi}{450}x - t\right)} $$
$$ E_{\mathrm{green}} = E_z \cos{\left(\frac{2\pi}{680}x - t\right)} $$
를 더한 것이 500nm의 plane wave가 되는 것은 아니다.
$$ E_{\mathrm{blue}} + E_{\mathrm{green}} = E_z \left[ \cos{\left(\frac{2\pi}{450}x - t\right)} + \cos{\left(\frac{2\pi}{680}x - t\right)} \right] \ne E_z' \cos{\left(\frac{2\pi}{500}x-t\right)} = E_{\mathrm{aqua}} $$
image by Wolfram Mathematica
여러 색을 섞어서 다른 색을 만들어 내는 것은, 단순히 plane wave를 더하는 것이 아니라, 인간의 눈이 색을 인식하는 메커니즘(3종류의 색 인지 세포들을 자극)에 의해 일어나는 현상이다. 물리적으로 [파란색+초록색]의 빛과 순수한 aqua색의 빛은 다른 electromagnetic field이지만, 눈에 들어오는 자극은 동일하기 때문에 색을 똑같이 인식한다는 것이다. 따라서 빛과 색에 대하여 과학적, 정량적으로 다루기 위해서는 물리적인 빛과 인간의 색 인식 사이의 구조를 파악하는 것이 필수이다.
이번 페이지에서는 물리적 현상인 electromagnetic field와 색, 그리고 인간의 색 인식과 표현이 대수적으로 어떤 구조를 가지고 연결되는지 살펴보자.
#Grassmann Structure
집합 \( \mathcal{A} \)를 모든 spectral energy distribution의 집합이라고 하자. 임의의 electromagnetic field는 Fourier transformation에 의해
$$ \vec{E}(\vec{r},t) = \int _{\mathbb{R}^3} \vec{f}(\vec{k}) e^{-i(\vec{k} \cdot \vec{r} - \omega t)} ~d^3 k $$
로 표현되는데 우리가 관심있는 영역은 wavelength가 380~800nm인 영역에서의 \( |\vec{f}(\vec{k})|^2 \)이므로, 그 외의 영역에 대해서는 equivalence class들로 묶어 집합 \( A \)를 만들 수 있다.
$$ A = \left\{~ f(\lambda) ~~\left|~~ f(\lambda) \ge 0 ~,~ \int |f(\lambda)|^2 ~d\lambda < \infty \right. ~\right\} $$
즉, 집합 \( A \)는 유한한 에너지를 가지는 가시광선 영역의 스펙트럼 에너지 분포들의 집합이다. \( A \)가 함수들의 집합이므로 자연스럽게 함수의 addition과 scalar multiplication을 정의할 수 있다. 다만, addition과 multiplication이 \( A \)에 닫혀 있어야 하므로 addition과 scalar multiplication이 ring이 되지는 못하고 addition에 대해서는 commutative cancellation semigroup이 되고, scalar multiplication에 대해서는 ring과 비슷한 구조가 된다.
1. \( <A,\oplus> \), 모든 \(a\), \(b\), \(c \in A \) 에 대하여 다음이 성립한다. (commutative cancellation semigroup)
① \( a \oplus b \in A \)
② \( (a \oplus b) \oplus c = a \oplus (b \oplus c) \)
③ 만약 \( a \oplus c = b \oplus c \)이면 \( a = b \)
④ \( a \oplus b = b \oplus a \)
2. \( <A, \oplus , \ast> \), 모든 \( a,b \in A \), \( t \ge 0 \) 에 대하여 다음이 성립한다.
① \( t \ast a \in A \)
② \( t \ast ( u \ast a ) = (tu) \ast a \)
③ \( t \ast ( a \oplus b ) = (t \ast a ) \oplus (t \ast b) \)
④ \( ( t+u) \ast a = (t \ast a) \oplus (u \ast b) \)
⑤ \( 1 \ast a = a \)
여기에 Grassmann이 정립한 color의 특성들을 추가적으로 정의한다.
3. Law of equivalence
\( A \)에 equivalence relation \( \sim \) 를 정의하고 \( a, b \in A \)가 같은 color인 경우 \( a \sim b \) 라고 한다.
4. Law of additivity
$$ a \sim b ~~\Longleftrightarrow~~ (a \oplus c) ~\sim~ (b \oplus c) $$
5. Law of multiplication
$$ a \sim b ~~\Longrightarrow~~ (t \ast a) ~\sim~ (t \ast b) $$
6. Law of \( m \)-chromacy
① 임의의 \( a_0 , a_1, a_2, \cdots, a_m \in A \) 에 대하여 다음을 만족하는 \( t_i , u_i \)가 존재한다.
\( \sum _{i=0} ^m t_i \ast a_i \sim \sum _{i=0} ^m u_i \ast a_i \), 최소 한개의 \( i \)에 대하여 \( t_i \ne u_i \)
② 다음을 만족하는 \( a_1 \), \(a_2\), ..., \(a_m\) \in A \)가 존재한다.
만약 \( \sum _{i=1} ^m t_i \ast a_i \sim \sum _{i=1} ^3 u_i \ast a_i \) 이면 \( i=1,2,\cdots m \)에 대하여 \( t_i = u_i\) 이다.
(공백)
6-①은 일종의 dependent relation이고 6-②는 independent relation임을 알 수 있다. 보통 \( m=3 \)이면 6번 규칙은 additive color의 3원색을 수학적으로 표현한 것이다.
주의할 것은 Grassmann의 color 특성(3~6번의 특징)들은 항상 성립하는 것은 아니다. 예를 들어 같은 빛이라도 망막의 어떤 영역에 비춰지느냐에 따라 다른 color로 인식될 수 있고 (즉, \( a \sim a \)가 성립하지 않음) 아주 강한 밝기의 빛은 어떤 파장이든 하얗게 보인다. 그러나 이러한 극한적인 상황을 제외한 통상적인 경우에 Grassman의 특성은 성립한다. 즉, 이 페이지의 논의는 극한이 아닌 보통의 상황에서 적용될 수 있는 구조이다.
#Representation of Grassmann Structure
Group의 구조가 vector space로 representation될 수 있는 것처럼 semigroup(group의 subset이므로) 역시 vector space(의 subset)로 representation될 수 있다. 다만 문제는 Grassmann이 정립한 구조가 유지되도록 하는 representation이 존재하는가 이다. 이러한 representation을 구하기 위해 먼저 color의 "뺄셈"을 정의해야 한다.
\( A \times A = \{~ (a,b) ~|~ a,b \in A ~\} \)에 정의되는 연산 \(\approx\) 를 다음과 같이 정의한다.
\( a \oplus b' \sim a' \oplus b \)이면 \( (a,b) \approx (a',b') \)
(공백)
\( \oplus \)를 빛들 사이의 덧셈으로 생각한다면 \( (\cdot,\cdot) \) 은 일종의 뺄셈이라고 생각할 수 있다. 또한 \( \approx \)는 equivalence relation이므로 equivalence classes
$$ V = (A \times A) ~/ \approx $$
를 정의하고 여기에 addition과 scalar multiplication을
$$ [a,b] + [c,d] = [a \oplus c , b \oplus d ] $$
$$ t \cdot [a,b] = \left\{ \begin{matrix} [t \ast a , t \ast b] & \mathrm{if} & t>0 \\ [a,a] & \mathrm{if} & t=0 \\ [(-t) \ast b, (-t) \ast a] & \mathrm{if} & t<0 \end{matrix} \right. $$
으로 정의하면 \( <V,+,\cdot> \)은 vector space가 된다. 이제 \( A \)의 원소 \( e \)를 하나 택하여 함수 \( \phi : A \to V \) 를
$$ \phi (a) = [a \oplus e , e] $$
로 정의하면
$$ \phi (a \oplus b ) = \phi (a) + \phi (b) $$
$$ \phi (t \ast a) = t \cdot \phi (a) $$
즉, \( \phi \)는 \( A \)에서 \( V \)로의 homomorphism임을 알 수 있다. 이때 \( \phi \)는 원소 \( e \)에 independent함을 쉽게 보일 수 있다. 따라서 다음과 같은 결론을 얻는다.
\( <A,\oplus,\ast,\sim> \) 를 Grassmann structure라고 하자. 그러면 \( A \)의 image가 \(m\)-dimensional vector space \( V \)의 convex cone subset \( C \)가 되는 homomorphism \( \phi \)가 유일하게 존재한다.
CIE 1931, CIE 1960, L*a*b*와 같은 color space, 색맹에 대한 reduction dichromacy, red/green(또는 yellow/blue) cancellation equivalence과 같은 opponent colors theory 등은 이러한 대수적 관점에서 이해하고 분석할 수 있다.
'Etc > 디스플레이 공학 기초' 카테고리의 다른 글
| [색채학] 2. 빛의 물리적 특성과 색의 형성 (0) | 2020.10.18 |
|---|---|
| [색채학] 1. 디스플레이 장치의 기본 원리 (0) | 2020.10.16 |