통계 모델을 세우고 무작위 샘플링을 할 때, 경우에 따라서는 가장 작은 값이나 가장 큰 값, 또는 딱 중간 위치에 있는 값들에 대하여 관심이 있을 수 있다. 예를 들어, 가스가 분출되는 관을 설계를 할 때, 가스가 분출되는 가장 큰 압력을 견딜 수 있도록 설계하기 위해서는 실험의 최대값에 대하여 관심이 있을 것이다. 또한 분포가 상당히 비대칭적인 경우 이러한 분포를 대표하는 값으로 평균 대신 사용하는 중앙값이 중간 위치에 있는 샘플링 결과라고 할 수 있다. 이번 페이지에서는 이렇게 샘플링 값의 순서에 대한 값인 order statustics에 대하여 살펴본다.
# Order Satstistics
DEFINITION Order Statistics
Random sample \(X_1\), \(X_2\), ..., \(X_n\) 을 크기 순으로 다시 정리한 random sample을 \(X_1\), \(X_2\), ..., \(X_n\) 의 ordered statistics라고 부른다. 작은 순서부터 \(X_{(1)}\), \(X_{(2)}\), ..., \(X_{(n)}\) 로 표기한다.
즉, \(X_{(1)}\) 은 \(X_1\), \(X_2\), ..., \(X_n\) 중에서 가장 작은 수, \(X_{(2)}\) 는 2번째로 작은 수, \(X_{(j)}\) 는 j번째로 작은 수가 된다. \(X_{(n)}\) 은 n번째로 작은 수, 즉, 가장 큰 수가 된다. 이러한 order statistics를 이용하여 가장 큰 statistics와 가장 작은 statistics의 비율 \(X_{(n)} / X_{(1)}\) 과 같은 다양한 statistics를 만들어 낼 수 있다. 그 중에서 몇몇 statistics는 다음과 같이 특별한 이름으로 부른다.
1. Sample Range
\[ R = X_{(n)} - X_{(1)} \]
random sample 중 가장 큰 값과 가장 작은 값의 차이로 샘플들이 얼마나 멀리 분산되어 있는지를 표현하는 하나의 지표가 될 수 있다.1
2. Sample Median
\[ M = \left\{ \begin{array}{ll} X_{\left( \frac{n+1}{2} \right)} & \text{if }n \text{ is odd} \\ \\ ( X_{\left( \frac{n}{2} \right)} + X_{\left( \frac{n}{2}+1 \right)} ) / 2 & \text{otherwise.} \end{array} \right. \]
random sample 중 크기 순위가 정중앙에 있는 값이다. 다만, \(n\) 이 홀수인 경우에는 크기 순위가 정중앙인 값이 정확히 정해지지만, \(n\) 이 짝수인 경우에는 불명확하므로 정중앙의 양쪽의 평균값으로 잡는다. 예를 들어, random sample의 개수가 6개인 경우, 정중앙이 양쪽은 3번째 수와 4번째 수이므로 이 값들의 평균값이 sample median이 된다. sample mean과 sample median의 차이는 mean과 median의 차이와 비슷하다. 예를 들어, 대한민국 1인당 평균 GDP가 3만달러(약 3600만원)이라고 해서 평범한 4인 가정의 1년 수입이 1억 4천만원이라고 생각하는 것은 현실에 맞지 않을 것이다.
3. Sample Midrange
\[ V = \frac{X_{(1)} + X_{(n)}}{2} \]
random sample 중 가장 큰 값과 가장 작은 값의 평균값이다. sample median과 마찬가지로 분포를 대표하는 값으로 생각할 수 있다.
4. Sample Percentile
다음의 값을 \((100p)\)th sample percentile이라고 부른다. ( \(\{k\}\) 는 \(k\)의 반올림)
\[ \begin{array}{ll} X_{(\{np\})} & \text{if } \frac{1}{2n} < p < \frac{1}{2} \\ \\ X_{(n+1-\{n(1-p)\})} & \text{if } \frac{1}{2} < p < 1-\frac{1}{2n} \end{array} \]
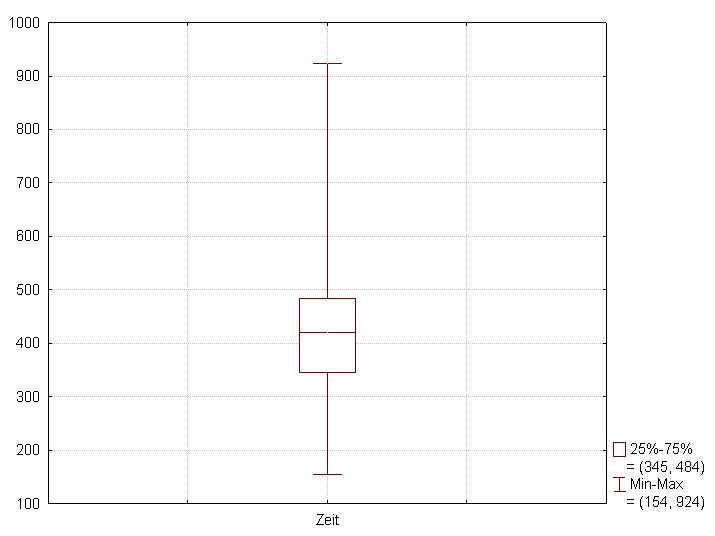
흔히 '75% 백분위'와 같이 부르는 statistics이다. 예를 들어 random sample의 개수가 10개인 경우, 75th sample percentile은, \(p=0.75\) 이므로 \(10+1-\{10\times(1-0.75)\} = 8\), 따라서 8번째로 작은 random sample 값이 된다. 25th percentile을 lower quartile, 75th percentile을 upper quartile, 이 두 값의 차이를 interquartile range라고 부르기도 한다. 이러한 용어는 분포를 box plot으로 표현할 때 많이 쓰인다. Box plot에 사용되는 그래프는 아래와 같은 모양으로 표현되는데, 각 선의 위치가 최소값, lower quartile, median, upper quartile, 최대값을 표현한다.

아래 그래프는 최소값 154, lower quartile 345, median 410, upper quartile 484, 최대값 924인 분포를 표현한다.
© Schlurcher From Wikimedia Commons
#Distribution of Order Statistics
Order statistics도 statistics이기 때문에 random variable, 즉, 어떤 정해진 값이 아니라 확률분포를 가지는 값이다. 샘플링을 통해 하나의 값으로 결정되는 과정은 이러한 random variable이 realization되는 것이라는 것을 기억하자. 그렇다면 주어진 모분포에서 무작위 샘플링을 했을 때, order statistics의 분포를 구할 수 있을까? 다음 정리를 살펴보자.
THEOREM
\(X_1\), \(X_2\), ..., \(X_n\) 을 discrete population \(f_X(x_i) = p_i\) 에서 추출한 random sample이라고 하고 \(x_1 < x_2 < \cdots \) 를 pmf에서 가능한 \(X\) 값을 순서대로 나열한 것이라고 하자. 또한 다음의 값들을 정의하자.
\[ \begin{array}{ccl} P_0 & = & 0 \\ P_1 & = & p_1 \\ P_2 & = & p_1 + p_2 \\ & \vdots & \\ P_i & = & p_1 + p_2 + \cdots + p_i \\ & \vdots & \end{array} \]
그러면 ordered statistics의 분포는 다음과 같이 구할 수 있다.
\[ \begin{equation} P\left( X_{(j)} \le x_i \right) = \sum_{k=j} ^n \left( \begin{array}{c} n \\ k \end{array} \right) \left[ P_i ^k (1-P-i) ^{n-k} - P_{i-1} ^k (1-P_{i-1}) ^{n-k} \right] \end{equation} \]
\[ \begin{equation} P\left(X_{(j)} = x_i \right) = \sum_{k=j} ^n \left( \begin{array}{c} n \\ k \end{array} \right) \left[ P_i ^k (1-P_i) ^{n-k} - P_{i-1} ^k (1-P_{i-1}) ^{n-k} \right] \end{equation} \]
(증명)
먼저 \(P_i\) 의 의미를 생각해보자. \(P_i = p_1 + p_2 + \cdots + p_i = f_X(x_1) + f_X(x_2) + \cdots + f_X(x_i)\) 이므로 \(P_i = P(X \le x_i)\), 즉, \(X\) 가 \(x_i\) 작거나 같을 확률이 된다. 이를 이용하면, k번째 sample \(X_k\) 가 \(x_i\) 보다 작을 확률은 결국 \(P_i\) 확률을 가진 Bernoulli trial2이 된다. 따라서, n개의 random sample 중에 k개의 sample만 \(x_i\) 보다 작거나 같고 다른 sample들은 \(x_i\)보다 클 확률은 binomial distribution이 된다.
\[ P(\text{only }k\text{ samples} \le x_i ) = \left( \begin{array}{c} n \\ k \end{array} \right) P_i ^k (1-P_i )^{n-k} \]
이제 event \(\{ X_{(j)} \le x_i \}\)를 생각해보자. random sample 중에 j번째로 작은 sample이 x_i보다 작을 경우는,
1. \(X_{(1)}\), ..., \(X_{(j)} \le x_i\) 이고 \(X_{(j+1)}\), \(X_{(j+2)}\), ..., \(X_{(n)} > x_i\)
2. \(X_{(1)}\), ..., \(X_{(j+1)} \le x_i\) 이고 \(X_{(j+2)}\), ..., \(X_{(n)} > x_i\)
⁞
3. 모두 \(X_{(n)} \le x_i\)
가 될 것이다. 즉,
1. j개의 sample만 \(x_i\) 보다 작거나 같다.
\[ P(\text{only }j\text{ samples} \le x_i ) = \left( \begin{array}{c} n \\ j \end{array} \right) P_i ^j (1-P_i) ^{n-j} \]
2. j+1개의 sample만 \(x_i\) 보다 작거나 같다.
\[ P(\text{only }j+1\text{ samples} \le x_i) = \left( \begin{array}{c} n \\ j+1 \end{array} \right) P_i ^{j+1} (1-P_i) ^{n-(j+1)} \]
⁞
3. n개의 sample이 \(x_i\) 보다 작거나 같다.
\[ P(n\text{ samples} \le x_i) = \left( \begin{array}{c} n \\ n \end{array} \right) P_i ^n (1-P_i) ^{n-n} \]
가 된다. 따라서 이 event의 확률은
\[ P(X_{(j)} \le x_i) = \sum _{k=j} ^n \left( \begin{array}{c} n \\ k \end{array} \right) P_i ^k (1-P_i) ^{n-k} \]
그리고 이 확률은 \(X_{(j)}\) 의 cdf의 정의이므로, cdf와 pmf와의 관계로부터
\[ P(X_{(j)} = x_i) = P(X_{(j)} \le x_i) - P(X_{(j)} \le x_{i-1}) = \sum _{k=j} ^n \left( \begin{array}{c} n \\ k \end{array} \right) \left[ P_i ^k (1-P_i)^{n-k} - P_{i-1} ^k (1-P_{i-1}) ^{n-k} \right] \]
(증명 끝)
같은 방식으로 continuous distribution에 대해서도 구할 수 있다.
THEOREM
\(X_1\), \(X_2\), ..., \(X_n\) 을 pdf \(f_X(x)\), cdf \(F_X(x)\) 로 가지는 continuous population에서 추출한 random sample이라고 하자. 그러면 \(X_{(j)}\) 의 pdf는 다음과 같이 구할 수 있다.
\[ \begin{equation}f_{X_{(j)}}(x) = \frac{n!}{(j-1)!(n-j)!} f_X(x) \left[ F_X(x)\right]^{j-1} \left[ 1- F_X(x) \right]^{n-j} \end{equation} \]
(증명)
전체적인 논리는 discontinuous 경우와 동일하다. 다만, k번째 sample \(X_k\) 가 \(x_i\) 보다 작을 확률을 나타냈던 \(P_i\) 가 이 경우에는 cdf \(F_X(x)\) 가 된다. 따라서, event \(\{ X_{(j)} \le x \}\) 의 확률은
\[ P(X_{(j)} \le x) = \sum _{k=j} ^n \left( \begin{array}{c} n \\ k \end{array} \right) [F_X(x)]^k [ 1- F_X(x)] ^{n-k} \]
그리고 이 확률은 \(X_{(j)}\) 의 cdf이므로 pdf는
\[ f_{X_{(j)}}(x) = \frac{d}{dx} P(X_{(j)} \le x) \]
를 이용하여 얻을 수 있다.
(증명 끝)
Example
0부터 1사이의 uniform distribution에서 99개의 random sample을 추출하였을 때, 크기 순으로 50번째에 있는 sample의 분포를 구해보자. 이 분포의 pdf는 \(f_X(x) = 1\), cdf는 \(F_X(x)=x\) 이므로
\[ f_{X_{(50)}}(x) = \frac{99!}{(50-1)!(99-50)!} x^{50-1} (1-x)^{99-50} = \frac{\Gamma(100)}{\Gamma(50)\Gamma(50)}x^{50-1} (1-x)^{50-1} \]
즉, beta(50,50) 분포가 된다. 이 분포의 expectation은 \(\frac{1}{2}\), variance는 \(\frac{1}{404}\) 이다. Random sample 중 크기 순으로 한 가운데 있는 값의 기대값이 0.5인 것은 쉽게 예측할 수 있을 것이다.
(예제 끝)
위 정리를 증명했던 논리를 조금 변형하면, order statistics의 joint pdf도 구할 수 있다.
THEOREM
\(X_1\), \(X_2\), ..., \(X_n\) 을 pdf \(f_X(x)\), cdf \(F_X(x)\) 로 가지는 continuous population에서 추출한 random sample이라고 하자. \(1\le i < j \le n\)일 때, \(X_{(i)}\), \(X_{(j)}\) 의 joint pdf는
\[ \begin{align*} f_{X_{(i)},X_{(j)}}(u,v) = &\frac{n!}{(i-1)!(j-1-i)!(n-j)!}f_X(u)f_X(v) \\ \\ & \times [F_X(u)]^{i-1}[F_X(v)-F_X(u)]^{j-1-i}[1-F_X(v)]^{n-j} \end{align*} \]
(단, \(u<v\))
- 이런 설명들을 만났을 때 항상 명심해야 할 것은, 이 값이 원래 표현하고자 하는 사실을 나타내는 유일한 지표가 아니라는 것이다. 샘플들이 얼마나 멀리 분산되어 있는지 표현하는 지표는 sample range 외에도 여러가지가 가능하며 각자의 장단점이 있기 때문에 목적과 상황에 맞는 것을 선택해서 사용해야 한다. [본문으로]
- 3.2 베르누이 분포, 이항 분포 Bernoulli Distribution, Binomial Distribution 참고 [본문으로]
'Mathematics > 통계학' 카테고리의 다른 글
| [통계학] 5.3-(2) 큰 수의 법칙 Law of Large Numbers (1) | 2022.04.27 |
|---|---|
| [통계학] 5.3-(1) 확률 변수의 수렴 Convergence of Random Variables (0) | 2022.03.02 |
| [통계학] 5.2-(3) F 분포 F-distribution (0) | 2021.08.17 |
| [통계학] 5.2-(2) 스튜던트 t 분포 Student's t-distribution (0) | 2021.08.16 |
| [통계학] 5.2-(1) Example: 정규 분포에서의 샘플 평균, 샘플 분산 Sample mean and Sample variance of Random sample from Normal Distribution (0) | 2021.08.11 |
| [통계학] 5.2 통계량, 샘플 평균, 샘플 분산 Statistic, Sample Mean and Sample Variance (0) | 2021.08.11 |