[통계학] 5.3-(2) 큰 수의 법칙 Law of Large Numbers

주사위를 몇번 던졌을 때 샘플 평균은 실제로 주사위 값이 얼마가 나왔느냐에 따라서 다르겠지만, 수천번, 수만번 던졌을 때 샘플 평균이 어떻게 될것 같나고 물어본다면 아마 3.5 정도 될 것이라고 말할 것이다. 다음 그림은 주사위를 500번 던졌을 때까지 샘플 평균을 시뮬레이션 해본 그래프이다.

주사위를 던져서 나온 수의 샘플 평균의 변화, 색깔마다 하나의 실험

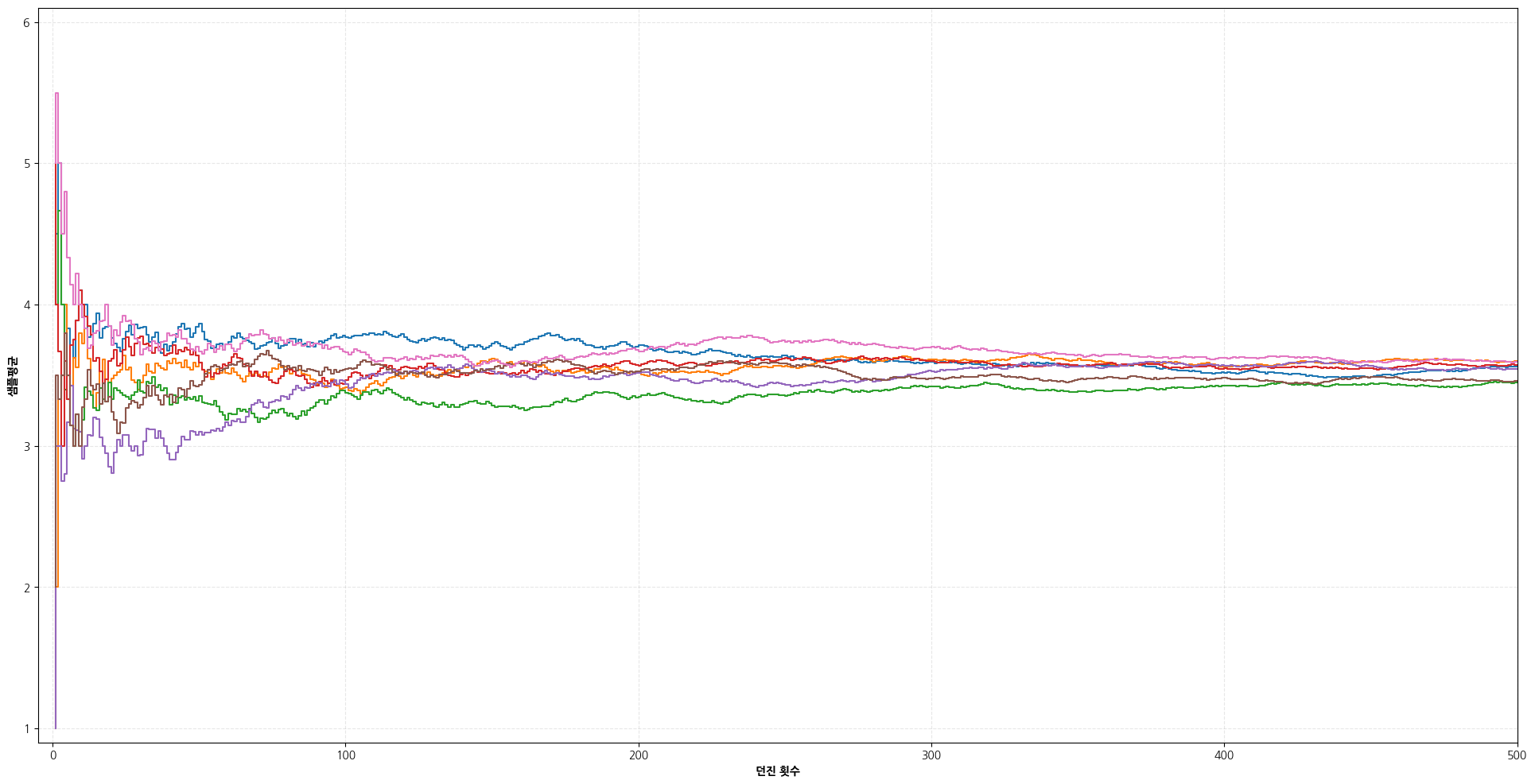
주사위를 던진 횟수를 약 10만번까지 시뮬레이션해보면 샘플 평균은 대부분 3.497~3.51 사이 값을 가진다. 따라서 주사위의 샘플 평균은 던진 횟수가 커질수록 3.5에 수렴한다고 할 수 있다.

 

그렇다면 3.5라는 값은 어디에서 나온 것일까? 아마 대부분 이렇게 생각했을 것이다.

 

"1이 나올 확률은 1/6, 2가 나올 확률은 1/6, ..., 6이 나올 확률은 1/6이므로 평균은 1ⅹ1/6 + 2ⅹ1/6 + ... + 6ⅹ1/6 = 3.5
따라서 주사위를 던진 횟수가 커진다면 샘플 평균은 3.5가 될거야!"

 

그러나 이 논리에는 커다란 허점이 있다. 방금 구한 1ⅹ1/6 + 2ⅹ1/6 + ... + 6ⅹ1/6 식은 확률 개념으로 기대값이다. 기대값은 한번 시도했을 때 나올 수 있는 수의 대표값이다. 그러나 샘플 평균은 통계 개념으로, 지금까지 나온 값들을 더해서 지금까지 수행한 횟수로 나눈 것이다. 5.2 통계량, 샘플 평균, 샘플 분산 Statistic, Sample Mean and Sample Variance에서 나왔던 정리를 이용하여 샘플 평균의 기대값이 주사위를 한번 던졌을 때의 기대값과 같으므로 문제가 없다고 할수도 있을 것이다. 그러나 이것 역시 성립하지 않는다. 예를 들어, 주사위를 n번째 던졌을 때 나오는 수를 $A_n$이라고 한다면, $E[A_n]=3.5$ 이므로 n이 계속 커지면 $A_n$ 이 3.5로 수렴한다고 하는 것과 같다. 그러나 그런 일은 일어나지 않는다. n번째 던졌을 때 나오는 수는 1부터 6까지의 자연수이며 3.5에 별로 가까워지지도 않는다. 즉, 확률 변수의 수열 $X_1$, $X_2$, ... 이 각각 기대값 $\mu$를 가진다고 해서 $X_n$이 n이 커짐에 따라 $\mu$에 수렴한다고 결론내릴 수 없다.

 

따라서 주사위의 샘플 평균이 던진 횟수가 커질수록 3.5에 수렴한다고 하기 위해서는 "확률 변수의 수열 $X_1$, $X_2$, ... 이 각각 기대값 $\mu$를 가질 때, 샘플 평균 ${\bar{X}}_n=\frac{1}{n}\sum _{i=1}^n{X}_i$ 는 n이 커질수록 $\mu$에 수렴한다"는 사실이 필요하다. 이를 the Law of Large Numbers(큰 수의 법칙)라고 부른다. (이하, LLN)

 

이번 페이지에서는 두 가지 버전의 LLN에 대해서 살펴본다.

 

THEOREM               The Weak Law of Large Numbers
$${\bar{X}}_n\stackrel{p}{\to }\mu$$

 

여기에서는 $\text{Var}(X_i)={\sigma }^2$ 으로 유한한 값을 가질 경우만 증명한다. 그러나 일반적으로 LLN(weak와 strong 모두)은 무한한 variance에서도 성립한다. variance가 무한한 경우에는 유한한 경우보다 더 천천히 수렴하게 될 뿐이다.

 

(증명)

$P(|{\bar{X}}_n-\mu |>ϵ)=P(({\bar{X}}_n-\mu {)}^2>{ϵ}^2)$이므로 Chebychev's inequality를 이용하면

$$P(({\bar{X}}_n-\mu {)}^2>{ϵ}^2)\le \frac{E[({\bar{X}}_n-\mu {)}^2]}{{ϵ}^2}=\frac{\text{Var}\left({\bar{X}}_n\right)}{{ϵ}^2}$$

이 때, 5.2 통계량, 샘플 평균, 샘플 분산 Statistic, Sample Mean and Sample Variance의 결과 $\text{Var}\left({\bar{X}}_n\right)={\sigma }^2/n$을 이용하면

$$P(|{\bar{X}}_n-\mu |>ϵ)\le \frac{{\sigma }^2}{n{ϵ}^2}$$

따라서 $n\to \mathrm{\infty }$ 이면, $P(|{\bar{X}}_n-\mu |>ϵ)\to 0$ 즉, ${\bar{X}}_n$은 $\mu$에 converge in probability한다.

(증명 끝)

 

THEOREM               The Strong Law of Large Numbers
$${\bar{X}}_n\stackrel{a.s.}{\to }\mu$$

 

Weak LLN은 convergence in probability의 정의상, $|{\bar{X}}_n-\mu |$ 가 $ϵ$보다 큰 경우가 무한히 발생할 수 있다. 그러나 almost surely convergent한 경우에는 이러한 일이 일어나지 않는다. 따라서 strong LLN이 성립하지 않지만 weak LLN이 성립하는 케이스들이 존재한다.(주로 expected value가 존재하지 않는 경우)