[통계학] 2.2-(1) 최빈값, 중앙값 Mode, Median

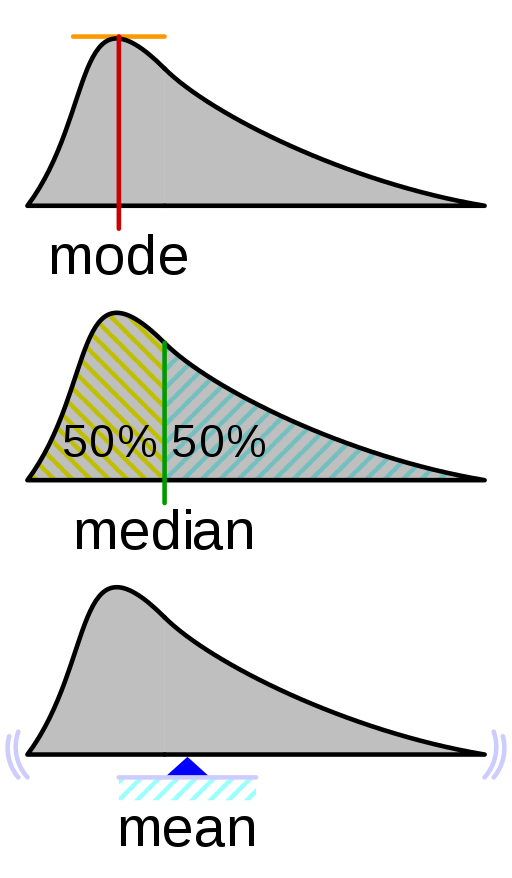
평균의 비슷한 개념으로 최빈값과 중앙값이 있다. 이번 페이지에서는 최빈값과 중앙값의 정의에 대하여 살펴본다.

 

Cmglee  /  CC BY-SA

 

#Mode

간단히 최빈값은 가장 빈번하게 나타날 수 있는 값을 의미한다.

 

DEFINITION            Modes of Distributions

 

Random variable $X$ 에 대하여 $f_X(x)$ 가 최대가 되는 값을 $X$의 mode(최빈값) 이라고 한다.

 

만약 random variable이 discrete한 경우에는 pmf가 바로 그 값이 될 확률이므로, $X$ 가 나올 확률이 가장 높은 $x$ 값이라고 할 수 있다. continuous의 경우에는 $X$가 $x$~$x+dx$ 의 값이 나올 확률이 가장 높은 $x$ 값이라고 해석 할 수 있다.

 

#Median

중앙값은 확률 분포에서 빈도상 정가운데 있는 값을 의미한다.

 

DEFINITION            Medians of Distributions

 

Random variable $X$에 대하여, $P(X\le m)=P(X\ge m)=\frac{1}{2}$ 인 $m$ 을 $X$ 의 median(중앙값)이라고 한다.

 

Random variable이 continuous인 경우에 위 식은

$${\int }_{-\mathrm{\infty }}^{m}f(x)dx={\int }_m^{\mathrm{\infty }}f(x)dx=\frac{1}{2}$$

가 된다.

 

Example

다음 분포에 대해서 최빈값과 중앙값을 구해보자.

$$f_X(x)=3x^2\text{where }0\le x\le 1$$
pdf가 증가함수이므로 당연히 $x=1$ 에서 $f_X$ 가 최대가 된다. 즉, 최빈값은 1이다.

중앙값을 구하기 위해서 직접 적분을 계산하면,
$${\int }_0^{m}3x^{2}dx=m^3$$
$${\int }_m^{1}3x^{2}dx=1-m^3$$
이므로 $m=\frac{1}{\sqrt[3]{2}}$ 이 중앙값이 된다.

 

#Comments

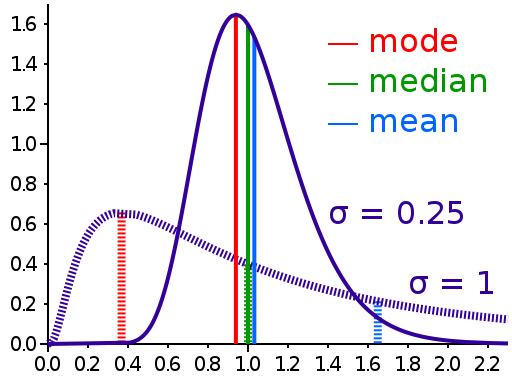
• 평균, 최빈값, 중앙값 모두 어떤 랜덤 변수의 대표값으로 사용할 수 있다. 특히 랜덤 변수의 분포가 대칭에 가까운 경우 이 세 값들은 비슷한 값을 나타낸다. 그러나 대칭에서 많이 벗어난 경우 세 값들 사이는 큰 차이가 있기 때문에 랜덤 변수의 대표로 어떤 것을 선택할지는 목적에 맞게 선택해야 한다. 다음 그림은 이 세 값의 차이를 나타낸다.

Cmglee  /  CC BY-SA

• Random variable이 연속인 경우,
  $$E[|X-a|]$$
  가 최소가 되도록 하는 $a$ 는 중앙값이 된다.
  
  이를 증명하기 위해서, expected value의 정의로부터
  $$E[|X-a|]={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}|x-a|f(x)dx={\int }_a^{\mathrm{\infty }}(x-a)f(x)dx+{\int }_{-\mathrm{\infty }}^a(a-x)f(x)dx$$
  이므로, $a$ 에 대한 미분
  $$\frac{d}{da}{\int }_a^{\mathrm{\infty }}(x-a)f(x)dx$$
  에 대하여 생각해보자. 일단, random variable의 support가 유한한 경우, $(x-a)f(x)$ 가 continuous이므로 미분과 적분의 순서를 바꾸는데 문제가 없다. support가 유한하지 않은 경우에는, 적분
  $${\int }_a^{\mathrm{\infty }}\frac{\partial }{\partial a}(x-a)f(x)dx$$
  가 uniformly convergent하면, 미분과 적분의 순서를 바꿀 수 있다. 여기에서는 위의 적분이 uniformly convergent하다고 가정한다. 따라서, $\frac{d}{da}E[|X-a|]$ 의 각 항의 적분과 미분의 순서를 바꿔 계산하면,
  $$\frac{d}{da}E[|X-a|]={\int }_a^{\mathrm{\infty }}-f(x)dx+{\int }_{-\mathrm{\infty }}^{a}f(x)dx$$
  이고, 전체 확률은 1이라는 점을 이용하여
  $${\int }_a^{\mathrm{\infty }}f(x)dx=1-{\int }_{-\mathrm{\infty }}^{a}f(x)dx$$
  를 대입하면,
  $$\frac{d}{da}E[|X-a|]=2{\int }_{-\mathrm{\infty }}^{a}f(x)dx-1$$
  이다. 최소가 되는 $a$ 에서는 위의 값이 0이어야 하므로,
  $${\int }_{-\mathrm{\infty }}^{a}f(x)dx=\frac{1}{2}$$
  즉, $a$ 값은 중앙값이어야 한다. 이 값에서 최소인지 확인하기 위해서 $a$ 에 대한 2계 미분을 살펴보면,
  $$\frac{d^2}{d{a}^2}E[|x-a|]=f(a)+f(a)\le 0$$
  이므로 최소임을 알 수 있다.
  
  
• 평균은 (존재하는 경우) 유일하지만, 최빈값과 중앙값은 유일하지 않을 수 있다. 예를 들어, pdf가
  $$f_X(x)=\{\begin{array}{cl}\frac{1}{2}& \text{if }0\le x\le 1\\ \frac{1}{2}& \text{if }2\le x\le 3\\ 0& \text{otherwise}\end{array}$$
  인 경우, 최빈값은 0~1, 2~3의 모든 실수가 되고, 중앙값은 1~2의 모든 실수가 된다.