[통계학] 3.7 정규 분포 Normal Distribution

이번 페이지에서는 이론적으로 가장 중요한 분포인 normal distribution(정규 분포)에 대하여 알아본다. 또 다른 이름으로 Gauss distribution(가우스 분포), Gaussian distribution(가우시안 분포), Laplace-Gauss distribution(라플라스-가우스 분포) 등의 이름으로 부른다. normal distribution의 응용 범위는 자연과학, 공학, 사회과학의 모든 영역에 걸쳐 있을 정도로 광범위 하므로 이 페이지에서 모든 것을 다루는 것은 불가능하다. 이 페이지에서는 normal distribution의 정의와 pdf, 평균, 분산 등만 살펴보도록 한다.

 

#Normal Distribution

실수 $\mu$, 양수 $\sigma$ 에 대하여, 연속적인 랜덤 변수 $X$ 가 다음의 pdf를 가지는 경우 이를 '(parameter가 $\mu$ 와 ${\sigma }^2$인) normal distribution'이라고 한다.^[각주:1]

$$f_X(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}\text{-}\mathrm{\infty }<x<\mathrm{\infty }$$

랜덤 변수 $X$ 가 normal distribution을 따른다는 것을 줄여서 다음과 같이 표현한다.

$$X\sim \mathcal{N}(\mu ,{\sigma }^2)$$

 

#Gaussian Integral

실제로 $f_X$ 가 pdf이기 위해서는 다음의 2가지 조건을 만족해야 한다.^[각주:2]

 

1. $f_X(x)\ge 0$
   
   
2. ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{f}_X(x)dx=1$

첫번째 조건은 확률이 음수가 될 수 없다는 의미이고, 두번째 조건은 모든 확률을 더하면 1이 된다는 뜻이다. exponential 함수는 양수 함수이므로 첫번째 조건은 자연스럽게 만족된다. 두번째 조건을 만족하기 위해서는 다음을 보여야 한다.

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}dx=1$$

적분을 간단히 하기 위해서 새로운 변수 $t=\frac{x-\mu }{\sqrt{2}\sigma }$ 를 정의하면, $dt=\frac{1}{\sqrt{2}\sigma }dx$ 이므로, 위 식은 다음과 같이 압축된다.

 

 

THEOREM            Gaussian Integral

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-t^2}dt=\sqrt{\pi }$$

 

가장 이해하기 쉬운 증명은 극좌표를 이용한 것이다.

 

먼저 식 $\text{(???)}$ 의 좌변을 $I$ 라고 정의하고 $I$ 값을 구하기 위해 다음을 생각해보자.

$$I^2=\left({\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-x^2}dx\right)\left({\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-y^2}dy\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-(x^2+y^2)}dxdy$$

이 적분은 좌표평면 전체에 대한 적분이 된다. ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}dxdy$ 가 적분을 하는 방식은 $(x,y)$ 에서 가로의 길이가 dx, 세로의 길이가 dy인 직사각형 만들어, 먼저 x방향으로 $-\mathrm{\infty }$ 부터 $\mathrm{\infty }$ 까지 쌓고, 이를 다시 y방향으로 쌓는 것이다.^[각주:3]

 

이를 극좌표로 다시 나타내보자. $(r,\theta )$ 에서 $r$ 방향으로 $dr$ , $\theta$ 방향으로 $d\theta$ 만큼 커졌을 때 생기는 넓이는 $dr$ 과 $d\theta$ 가 매우 작기 때문에, 직사각형으로 근사할 수 있고 넓이는 $rd\theta dr$ 가 된다.

 

이 기본 단위를 먼저 $\theta$ 방향으로 쌓고, 이를 다시 $r$ 방향으로 쌓아서 좌표평면 전체를 나타낼 수 있다.

 

그리고 직교좌표와 극좌표의 관계

$$x=r\cos \theta$$

$$y=r\sin \theta$$

를 이용하면, $e^{-(x^2+y^2)}=e^{-r^2}$ 이 된다. 따라서 식 $\text{(???)}$는

$$I^2={\int }_0^{\mathrm{\infty }}{\int }_0^{2\pi }{e}^{-r^2}rd\theta dr$$

$r^2=t$ 로 치환하면,

$$I^2=2\pi {\int }_0^{\mathrm{\infty }}\frac{1}{2}{e}^{-t}dt=\pi$$

이므로

$$I=\sqrt{\pi }$$

 

변수를 치환하여 다음과 같은 결론을 얻을 수 있다.

 

COROLLARY            

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-a{t}^2}dt=\sqrt{\frac{\pi }{a}}\text{a}>0$$

 

#Moment Generating Function of Normal Distribution

Normal distribution에서 mgf를 구하는 것이 크게 어렵지 않으므로, 이를 이용해 평균과 분산을 구하도록 하자. Mgf는 정의^[각주:4]로부터

$$M_X(t)=E[e^{tX}]=\frac{1}{\sqrt{2\pi }\sigma }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{tx}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}dx=\frac{1}{\sqrt{2\pi }\sigma }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}+tx}dx$$

이 때,

$$\begin{array}{rl}-\frac{(x-\mu {)}^2}{2\sigma }+tx& =-\frac{1}{2{\sigma }^2}[(x^2-2\mu x+{\mu }^2-2{\sigma }^{2}tx]\\ \\ & =-\frac{1}{2{\sigma }^2}[x^2-2(\mu +{\sigma }^{2}t)x+{\mu }^2]\\ \\ & =-\frac{1}{2{\sigma }^2}[x^2-2(\mu +{\sigma }^{2}t)x+(\mu +{\sigma }^{2}t{)}^2-(\mu +{\sigma }^{2}t{)}^2+{\mu }^2]\\ \\ & =-\frac{1}{2{\sigma }^2}[{\{x-(\mu +{\sigma }^{2}t)\}}^2-2\mu {\sigma }^{2}t-{\sigma }^4{t}^2]\\ \\ & =-\frac{[x-(\mu +{\sigma }^{2}t){]}^2}{2{\sigma }^2}+\mu t+\frac{{\sigma }^2{t}^2}{2}\end{array}$$

이므로, 식 $\text{(???)}$는

$$M_X(t)=e^{\mu t+\frac{{\sigma }^2{t}^2}{2}}\frac{1}{2\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-\frac{[x-(\mu +{\sigma }^{2}t){]}^2}{2{\sigma }^2}}dx$$

이고, 마지막 적분은 Gaussian integral이므로

$$M_X(t)=e^{\mu t+\frac{{\sigma }^2{t}^2}{2}}$$

을 얻을 수 있다.

 

#Mean of Normal Distribution

Mgf를 $t$ 에 대하여 한번 미분하면

$$\frac{d}{dt}{M}_X(t)=(\mu +t{\sigma }^2)e^{\mu t+\frac{{\sigma }^2{t}^2}{2}}$$

이므로

$$E[X]={\frac{d}{dt}{M}_X(t)|}_{t=0}=\mu$$

따라서 normal distribution의 평균은 parameter $\mu$ 임을 알 수 있다.

 

#Variance of Normal Distribution

Mgf를 $t$ 에 대하여 두번 미분하면

$$\frac{d}{dt}{M}_X(t)=(\mu +t{\sigma }^2{)}^2{e}^{\mu t+\frac{{\sigma }^2{t}^2}{2}}+{\sigma }^2{e}^{\mu t+\frac{{\sigma }^2{t}^2}{2}}$$

이므로

$$E[X^2]={\frac{d^2}{d{t}^2}{M}_X(t)|}_{t=0}={\mu }^2+{\sigma }^2$$

따라서 normal distribution의 분산은

$$(X)=E[X^2]-E[X{]}^2={\sigma }^2$$

임을 알 수 있다.

 

#Graph of Normal Distribution

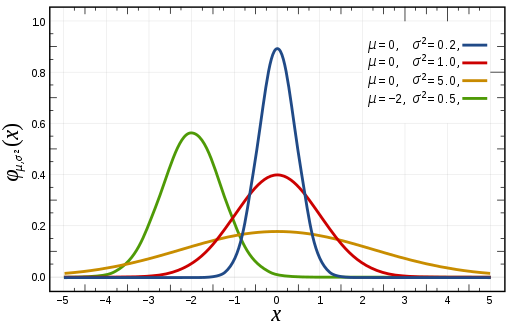
식 $\text{(???)}$를 살펴보면, exponential의 지수에 마이너스가 붙어있으므로 지수가 0일 때, 즉 $x=\mu$ 일 때 최대값을 가진다는 것을 알 수 있다. $x$ 가 $\mu$ 에서 벗어나면서, $\mu$ 보다 더 커지거나 아니면 작아지거나 상관없이, $\mu$ 에서 얼마나 떨어져 있는지에 따라 함수값이 점점 작아짐을 알 수 있다. $\mu$ 값이 normal distribution의 평균이므로, 결국 평균에서 벗어나면 벗어날 수록 점점더 함수값이 작아진다는 것을 알 수 있다. 이를 랜덤 변수 $X$ 로 해석하면, normal distribution을 따르는 랜덤 변수 $X$ 의 실제값을 측정했을 때, 평균 근처의 값이 나올 확률이 높고, 평균에서 많이 벗어나 있는 값이 나올 확률은 낮다는 뜻이 된다.

 

다른 parameter $\sigma$ 는 확률과 확률 분포에 어떤 영향을 줄까? 같은 평균 $\mu$ 를 가지지만 다른 parameter 값 ${\sigma }_1<{\sigma }_2$ 을 가지는 두 분포를 비교해보자. 먼저 $x=\mu$ 일 때 함수값은 각각 $\frac{1}{\sqrt{2\pi }{\sigma }_1}$ 과 $\frac{1}{\sqrt{2\pi }{\sigma }_2}$ 이므로 더 낮은 ${\sigma }_1$ 분포에서 함수값이 더 높다는 것을 알 수 있다. 즉, 더 낮은 $\sigma$ 값을 가질 수록, 평균 근처의 값이 나올 확률이 높다. 이제, $x$ 가 $\mu$ 에서 1만큼 벗어난 곳에서는 평균에서 함수값에 비해 얼마나 낮아지는지 살펴보자. 평균에서 함수값에 비하여, 함수값이 $e^{-\frac{1}{2{\sigma }^2}}$ 배가 되므로, $\sigma$ 값이 더 낮은 경우 함수값이 상대적으로 더 빨리 감소함을 알 수 있다. 즉, 더 낮은 $\sigma$ 값을 가질 수록, 평균에서 많이 벗어나 있는 값이 나올 확률이 빠르게 감소한다.

 

이러한 사실들을 그래프에서 직접 확인할 수 있다.

 

Inductiveload / Public domain via Wikimedia

 

같은 $\mu$ 값을 가지는 파란색, 빨간색, 오렌지색을 비교해보면, 가장 낮은 $\sigma$ 값을 가지는 파란색이 평균 근처에서 가장 높은 확률을 가지지만, 평균에서 벗어날 수록 가장 빠르게 확률이 감소하고, 가장 높은 $\sigma$ 값을 가지는 오렌지색이 평균 근처에서 가장 낮은 확률을 가지지만, 평균에서 벗어나도 감소하는 정도가 덜하다.

 

 

1. 여러 normal distribution을 다룰때는 혼동되지 않도록 parameter를 명시해 주는것이 좋다. [본문으로]
2. 1.6 확률 질량 함수, 확률 밀도 함수 Probability Mass Function, Probability Density Function 참고. [본문으로]
3. 정적분은 구분구적법의 극한이다. [본문으로]
4. 2.3 분산, 모멘트 생성 함수 Variance, Moment Generating Functions 참고. [본문으로]