어떤 현상과 현상 사이에 걸리는 시간이나 실험 횟수는 이 페이지에서 논의할 푸아송 분포로 모델링된다. 시간의 절대값보다는 기다린 시간의 길이가 사건이 벌어질 확률에 영향을 준다던지, 기다리는 시간이 길어질수록 사건 확률이 커지는 것과 같은 받아들일만한 가정들로 모델링하면 푸아송 분포를 얻게된다. 이번 페이지에서는 푸아송 분포의 정의와 평균, 분산 등을 살펴보고, 시간이 흐르면서 발생하는 사건 등을 모델링하는 방법을 살펴본다.
#Poisson Distributions
주어진 양수 \(\lambda\)에 대하여, 랜덤 변수 \(X\) 가 다음과 같은 pmf를 가질 때 이를 Poisson \((\lambda)\) distribution이라고 한다.
\[ f_X(x) = P(X=x) = e^{-\lambda}\frac{\lambda^x}{x!} ~~~~~ \text{where } ~ x=0,1,2,\cdots \]
이 함수가 pmf가 되는지 확인하기 위해, 총합이 1임을 확인해야 한다. Exponential function의 Tylor series
\[ e^x = \sum _{i=0} ^\infty \frac{x^i}{i!} \]
로부터
\[ \sum _{x=0} ^\infty f_X(x) = e^{-\lambda} \sum_{x=0} ^\infty \frac{\lambda^x}{x!} = e^{-\lambda}e^{\lambda} = 1 \]
을 확인할 수 있다. 랜덤 변수 \(X\)가 Poisson \((\lambda)\) distribution을 따른다는 것을 다음과 같이 표기한다.
\[ X \sim \mathrm{Pois}(\lambda) \]
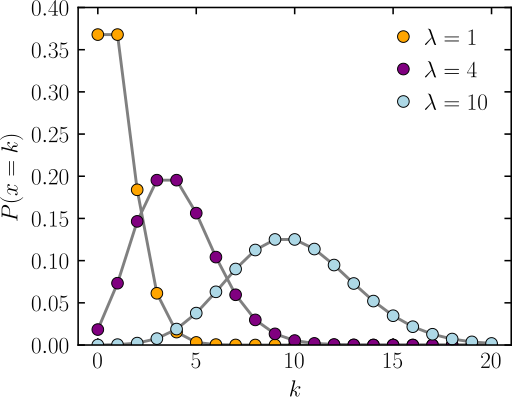
아래 그래프는 여러 \(\lambda\) 값에 대한 Poisson distribution의 pmf이다.
#Mean of Poisson Distribution
Exponential function의 Tylor series를 이용하면 Poisson distribution의 평균을 쉽게 구할 수 있다.
\[ \begin{align*} E[X] &= \sum _{x=0} ^\infty x e^{-\lambda}\frac{\lambda^x}{x!} \\ &= \sum _{x=1} ^\infty x e^{-\lambda}\frac{\lambda^x}{x!} & & {\scriptstyle \leftarrow ~ \text{omit } x=0} \\ &= \lambda e^{-\lambda} \sum_{x=1} ^\infty \frac{\lambda^{x-1}}{(x-1)!} \\ &= \lambda e^{-\lambda} \sum_{y=0} ^\infty \frac{\lambda^y}{y!} & & {\scriptstyle \leftarrow ~ \text{substitute } y=x-1} \\ &= \lambda e^{-\lambda} e^{\lambda} \\ \\ &= \lambda \end{align*} \]
#Variance of Poisson Distribution
같은 방식으로 분산도 구할 수 있다.
\[ \begin{align*} E[X^2] &= \sum _{x=0} ^\infty x^2 e^{-\lambda}\frac{\lambda^x}{x!} \\ &= \sum _{x=1} ^\infty x^2 e^{-\lambda}\frac{\lambda^x}{x!} & & {\scriptstyle \leftarrow ~ \text{omit } x=0} \\ &= \lambda e^{-\lambda} \sum_{x=1} ^\infty x\frac{\lambda^{x-1}}{(x-1)!} \\ &= \lambda e^{-\lambda} \left[ \sum _{x=1} ^\infty (x-1) \frac{\lambda^{x-1}}{(x-1)!} + \sum _{x=1} ^\infty \frac{\lambda^{x-1}}{(x-1)!} \right] \\ &= \lambda e^{-\lambda} \left[ \lambda \sum _{x=2} ^\infty \frac{\lambda^{x-2}}{(x-2)!} + \sum _{x=1} ^\infty \frac{\lambda^{x-1}}{(x-1)!} \right] & & {\scriptstyle \leftarrow ~ \text{omit } x=1 ~\text{in the first sum}} \\ &= \lambda e^{-\lambda} \left[ \lambda \sum _{z=0} ^\infty \frac{\lambda^{z}}{z!} + \sum _{y=0} ^\infty \frac{\lambda^{y}}{y!} \right] & & {\scriptstyle \leftarrow ~ \text{substitute } z=x-2 ~,~ y=x-1} \\ &= \lambda e^{-\lambda} [\lambda e^{\lambda} + e^{\lambda}] \\ \\ &= \lambda^2 + \lambda \\ \\ \mathrm{Var}(X) &= E[X^2] - (E[X])^2 \\ \\ &= \lambda^2 + \lambda - \lambda^2 = \lambda \end{align*} \]
#Moment Generating Function of Poisson Distribution
mgf 역시 같은 방식으로 구할 수 있다.
\[ \begin{align*} M_X(t) &= \sum _{x=0} ^\infty e^{tx} e^{-\lambda}\frac{\lambda^x}{x!} \\ &= e^{-\lambda} \sum _{x=0} ^\infty \frac{(\lambda e^t)^x}{x!} \\ &= e^{-\lambda}e^{\lambda e^t} \\ \\ &= e^{\lambda(e^t -1)} \end{align*} \]
#Poisson Limit Theorem
Binomial \((n,p)\) distribution에서 Bernoulli trial의 횟수 \(n\)이 엄청 커지고, Bernoulli trial의 '성공' 확률 \(p\)가 0에 매우 근접하는 경우 Poisson distribution으로 근사할 수 있다. \(X \sim B(n,p)\)의 pdf
\[ \begin{align*} f_X(x) &= \left( \begin{array}{c} n \\ x \end{array} \right) p^x (1-p)^{n-x} \\ &= \frac{n!}{x!(n-x+1)!} p^x (1-p)^{n-x} \\ &= \frac{1}{x!} n(n-1)\cdots(n-x+1) p^x (1-p)^{n-x} \end{align*} \]
에서 \(\lambda = np\) 로 정의하면,
\[ f_X(x) = \frac{1}{x!} [n^x + O(n)] \frac{\lambda^x}{n^x} \left(1- \frac{\lambda}{n} \right) ^{n-x} \]
이제 \(n \to \infty\)이므로 \((n-x) \to \infty\) , \(\frac{n^x + O(n)}{n^x} \to 1\) 그리고 exponential의 정의
\[ \lim _{n \to \infty} \left( 1 - \frac{\lambda}{n} \right) ^n = e^{-\lambda} \]
를 이용하면1
\[ f_X(x) \to e^{-\lambda}\frac{\lambda^x}{x!} \]
즉, Poisson distribution이 된다.
THEOREM Poisson Limit Theorem (Binomial ver.)
Binomial \((n,p)\) distribution에서 \(n \to \infty\), \(p \to 0\) 이고 그 곱 \(np=\lambda > 0\) 이면,
\[ B(n,p) \sim \mathrm{Pois}(\lambda) \]
보통 \(n \ge 20\) , \(p \le 0.05\) 또는 \(n \ge 100\) , \(np \le 10\) 에서 근사의 오차가 적다고 한다.
Example
전구 납품 업체에서 생산하는 전구는 대략 5000개 중에 1개의 불량품이 생긴다고 한다. 이 업체에서 10000개의 전구를 납품할 때, 불량품이 3개를 넘지 않을 확률은 얼마가 되는가? Binomial distribution의 결과와 Poisson distribution으로 근사한 결과를 비교해보자.
① Binomial Distribution
10000개의 전구에 대하여 불량품 검색이므로 \(n=10000\), 5000개 중에 1개의 불량품이 발생하므로 \(p=0.0002\)
\[ \begin{align*} P(X<3) &= \sum _{x=0} ^2 \left( \begin{array}{c} 10000 \\ x \end{array} \right) \times 0.0002^x \times 0.9998^{10000-x} \\ \\ &= 0.676~676~417~085~618 \end{align*} \]
② Poisson Distribution
\(\lambda = np = 2\)이므로
\[ P(X<3) = \sum _{x=0} ^2 e^{-2}\frac{2^x}{x!} = 0.676~676~416~183~064 \]
두 결과 사이의 차이가 0.000000001 정도로 거의 동일하다고 할 수 있다.
#Poisson Process
상담 센터에서 고객 불만을 전화로 접수하는 업무를 하는 상황이라고 하자. 전화 접수 횟수를 통계적으로 분석을 할 때 다음과 같은 특징을 예상할 수 있다.
① 업무 시작 순간에는 걸려온 전화 수가 없다.
② 겹치지 않는 시간대에 걸려온 전화 수는 서로 독립이다.
③ 걸려온 전화 수는 시간 길이에만 영향을 받는다.
④ 업무 시간이 짧을 때는 전화 수는 시간에 비례한다.
⑤ 동시에 여러 전화를 처리하지 않는다.
이를 수학적으로 모델링하면, \(t \ge 0\) 에 대하여, 랜덤 변수 \(N_t\) 를 업무 시작부터 t분까지 받은 전화의 수라고 하자. 그러면 위의 특징들을 다음과 같이 정리할 수 있다.
① \(N_0 = 0\)
② \(s < t\) 에 대하여, \(N_s\) 와 \(N_t - N_s\) 는 서로 독립적
③ \(N_s\) 와 \(N_{t+s} - N_t\) 는 서로 identically distributed
④ \(\lim _{t\to 0} \frac{P(N_t =1)}{t} = \lambda \)
⑤ \(\lim _{t\to 0} \frac{P(N_t >1)}{t} = 0 \)
이러한 특징을 가지는 사건을 Poisson process라고 부른다. 이 때 랜덤 변수 \(N_t\)는 Poisson \((\lambda t)\) distribution을 따른다. 여기에서 핵심이 되는 성질은 ③이다.
한 전화를 받고 다음 전화를 받을 때까지 걸린 시간을 \(X\)라고 하자. ③을 만족하기 위해서는
\[ P(X>t+x | X>t) = P(X>x)\]
이어야 한다. 즉, 한 전화를 받고 다음 전화를 기다린지 이미 \(t\) 분이 지났을 때, 여기에 더해 \(x\) 분이 지날 확률은, 독립적으로 한 전화를 받고 다음 전화를 기다린 시간이 \(x\) 분이 지날 확률과 동일해야 한다. 이러한 특성을 memoryless property라고 한다. 이미 \(t\) 분이 지난 것을 기억하지 않고 앞으로 \(x\) 분이 지날 확률만 조건부 확률에 영향을 미친다는 뜻이다.
DEFINITION Memoryless Property
랜덤 변수 \(X\) 가 \(P(X>0) = 1\) 이고, 임의의 양수 \(x\), \(t\) 에 대하여
\[ P(X>t+x) = P(X>x) P(X>t) \]
를 만족하는 경우, \(X\) 는 momoryless property를 가진다고 부른다.
이러한 특성을 가장 잘 반영하는 함수가 exponential 함수이다.
\[ P(X>x) = e^{-\lambda x} \]
Poisson process에서 exponential이 나타나는 것은 memoryless property 때문이다. 이로부터 유도되는 \(N_t\) 의 ③ 성질을 stationary increment property라고 한다.
Example
위의 전화 예에서, 평균적으로 5분에 3개의 전화가 걸려온다고 하자. 즉, \(\lambda = \frac{3}{5}\). 그러면 전화를 받고 다음 5분 동안 아무 전화도 걸려오지 않을 확률은 얼마일까? 위의 가정들로부터 전화를 받고 다음 5분 동안 전화가 걸려오지 않을 확률은 처음 5분 동안 전화가 걸려오지 않을 확률과 같으므로
\[ P(N_5 = 0 ) = e^{-\frac{3}{5} \times 5} \frac{(\frac{3}{5} \times 5)^0}{0!} = 0.0497871 \]
다음 1분 동안 전화가 2개 걸려올 확률은
\[ P(N_1 = 2 ) = e^{-\frac{3}{5} \times 1} \frac{(\frac{3}{5} \times 1)^2}{2!} = 0.395144 \]
Reference
Poisson Process
- 지수의 -k 부분은 \\(n \\to \\infty\\) 에서 1이 된다. [본문으로]
'Mathematics > 통계학' 카테고리의 다른 글
| [통계학] 3.6 균등 분포 Uniform Distribution (0) | 2020.08.17 |
|---|---|
| [통계학] 3.5 음이항 분포, 기하 분포 Negative Binomial Distribution, Geometric Distribution (0) | 2020.07.31 |
| [통계학] 3.4 초기하 분포 Hypergeometric Distribution (0) | 2020.07.25 |
| [통계학] 3.2 베르누이 분포, 이항 분포 Bernoulli Distribution, Binomial Distribution (2) | 2020.07.24 |
| [통계학] 3.1 이산 균등 분포 Discrete Uniform Distribution (0) | 2020.07.24 |
| [통계학] 2.3 분산, 모멘트 생성 함수 Variance, Moment Generating Functions (2) | 2020.07.24 |