디자인, 컴퓨터 그래픽 등에서 사용되는 원근법 등은 Euclidean space, 그리고 finite dimensional vector space에서 하나의 vector가 subspace에 자연스럽게 projection 될 수 있다는 사실에 기반한다. Hilbert space는 이러한 Euclidean space의 성질들이 유지된다. 이러한 개념은 Hilbert Projection Theorem에 집약되어 있다.
THEOREM Hilbert Projection Theorem
Hilbert space \(H\)와 proper subspace이면서 Hilbert space인 \(W\)와 주어진 \(x\in H\)에 대하여,
1. \( \left\| \hat{x}-x \right\| \le \left\| g-x \right\| \mathrm{~~for~all~}g\in W \)
2. \( \left\langle \hat{x}-x,g \right\rangle =0 \mathrm{~~for~all~}g\in W \)
를 만족하는 \(\hat{x}\in W\)가 유일하게 존재한다.
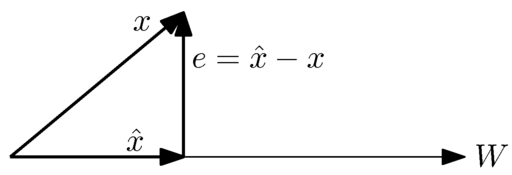
이 theorem의 의미를 아래의 그림으로 이해할 수 있다.
By Zvika [Public domain], from Wikimedia Commons
보통, \(\hat{x}\)를 \(x\)의 (\(W\)에서의) best approximation이라고 부른다. 이러한 개념들은 수치해석이나 통계학의 estimation 등으로 응용된다.(---page link--- 참고)
'Mathematics > 선형대수' 카테고리의 다른 글
| (선형대수학) 5.7 Gâteaux Derivative, Fréchet Derivative, Euler-Lagrange Equation (9) | 2018.08.13 |
|---|---|
| (선형대수학) 5.6 Classical Orthogonal Polynomials (0) | 2018.08.05 |
| (선형대수학) 5.5 Bounded Linear Functionals (0) | 2018.08.03 |
| (선형대수학) 5.3 \(L^2\) Space (0) | 2018.08.03 |
| (선형대수학) 5.2 Hilbert Space (0) | 2018.08.03 |
| (선형대수학) 5.1 Completeness (0) | 2018.08.02 |