이후로는 몇 페이지에 걸쳐서
$$ \frac{d^2}{dx^2}f(x)=kf(x) $$
와 같은 differential equation을 선형대수의 관점에서 분석하기 위해 필요한 도구들을 살펴볼 것이다. Differential equation을 이론적으로 분석하기 위해서는 해석학적 지식이 필요하지만 물리학과 학부생 입장에서는 해석학적 개념에 익숙하지 않기 때문에 여기에서 핵심이 되는 개념들만 설명하고 이후 페이지에서도 개략적으로만 설명할 것이다.
Differential equation 그리고 integral theory를 설명하기 위해서는 반드시 무한수열의 수렴에 대한 이해가 필요하다. 예를들어, Riemann integral은
$$ \int _a ^b f(x)dx = \lim _{n\to\infty} \sum_{i=1} ^n f\left(a+\frac{i-1}{n}(b-a)\right)\frac{b-a}{n} $$
과 같은 무한급수로 정의된다.(정확한 정의는 조금 더 복잡하다.) 만약 이 급수가 어떤 값에 수렴한다면 그 값이 곧 Riemann integral이 표현하는 함수 값과 x축 사이의 넓이가 된다.
Real number들의 sequence에서 convergence는 다음과 같이 정의된다.
Real number들의 sequence \(a_1\), \(a_2\), ... 가 고정된 real number \(L\), 모든 positive real number \(\epsilon\)에 대하여,
\(n>N\) 인 모든 \(a_n\)이 \(\left| a_n-L \right| < \epsilon\)
을 만족하는 \(N\)이 존재하는 경우 이 sequence가 convergent하다고 부르고 \(L\)에 converge한다고 부른다. 또한 이를
$$ \lim _{n\to\infty} a_n = L $$
로 표현한다.
Riemann integral과 같은 무한급수는
$$ \begin{array}{c} \begin{array}{lll} S_1 & = & f(a)(b-a) \\ S_2 & = & f(a)\frac{b-a}{2}+f(\frac{a+b}{2})\frac{b-a}{2} \end{array} \\ \vdots \end{array} $$
와 같이 수열로 만들어서 수렴을 확인할 수 있다.
Convegence와 비슷한 개념으로 Cauchy sequence라는 것이 있다.
Real number들의 sequence \(a_1\), \(a_2\), ... 가 모든 positive real number \(\epsilon\)에 대하여,
\(n,m>N\) 인 모든 \(a_n\), \(a_m\)이 \(\left|a_n-a_m\right| < \epsilon \)
을 만족하는 \(N\)이 존재하는 경우 이 sequence를 Cauchy sequence라고 부른다.
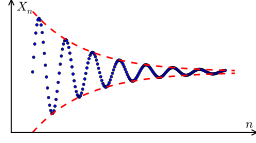
By Krishnavedala [CC0], from Wikimedia Commons
Cauchy sequence의 의미를 잘 살펴보면 \(n\)과 \(m\)이 커질 수록 \(a_n\)과 \(a_m\)의 차이가 점점 작아짐을 의미한다. 이는 \(n\)이 커질 수록 한 점에 접근한다는 convergent의 의미와 비슷해 보인다. 실제로, 어떤 real number들의 sequence가 convergent하면 자동적으로 Cauchy sequence가 된다. 역으로, 어떤 real number들의 sequence가 Cauchy sequence가 되면 자동적으로 convergent하다는 것이 증명되어 있다. 따라서 real number들의 sequece에서는 convergent와 Cauchy sequence가 동등한 의미이다.
real number들의 sequence의 convergent와 Cauchy sequence의 정의에서 사용한 수학적 개념은 절대값 \(\left| \cdot \right|\) 밖에 없으므로 절대값과 동일한 특징을 가진 연산이 정의된 집합에서는 모두 sequence의 convergent와 Cauchy sequence를 정의할 수 있다. 예를 들어, real number의 절대값은 norm의 일종이므로 Normed space에서 sequence의 convergent와 Cauchy sequence를 정의할 수 있다. (이후 norm을 \(\left\| \cdot \right\|\)로 표현함)
Normed space \(V\)의 vector들의 sequence \(\mathbf{v}_1\), \(\mathbf{v}_2\), ... 가 고정된 vector \(\mathbf{v}\), 모든 positive real number \(\epsilon\)에 대하여,
\(n>N\) 인 모든 \(\mathbf{v}_n\)이 \(\left\| \mathbf{v}_n - \mathbf{v} \right\| < \epsilon\)
을 만족하는 \(N\)이 존재하는 경우 이 sequence가 convergent하다고 부르고 \(\mathbf{v}\)에 converge한다고 부른다.
Normed space \(V\)의 vector들의 sequence \(\mathbf{v}_1\), \(\mathbf{v}_2\), ... 가 모든 positive real number \(\epsilon\)에 대하여,
\(n,m>N\) 인 모든 \(\mathbf{v}_n\), \(\mathbf{v}_m\)이 \(\left\| \mathbf{v}_n -\mathbf{v}_m\right\| < \epsilon \)
을 만족하는 \(N\)이 존재하는 경우 이 sequence를 Cauchy sequence라고 부른다.
Real number와 마찬가지로 어떤 sequence가 convergent하면 Cauchy sequence가 된다. 그러나 Real number와는 다르게 어떤 sequence가 Cauchy sequence라고 하더라도 반드시 convergent한 것은 아니다. 예를 들어 rational number 집합 \(\mathbb{Q}\)의 원소들로 구성된 sequence
1, 1.4, 1.41, 1.414, 1.4142, 1.41421, 1.414213, 1.4142135 , ...
는 Cauchy sequence이지만 어떠한 rational number로 converge하지 않는다. 사실 real number에서 보면 \(\sqrt{2}\)에 converge한다. 그러나 \(\sqrt{2}\)는 \(\mathbb{Q}\)의 원소가 아니다. 여기에서 rational number가 아닌 real number로 보면 되지 않느냐고 생각할 수 있겠지만, 일반적인 집합의 경우 Cauchy sequence가 반드시 convergent하지 않을 때 그렇게 되도록 해주는 더 큰 집합이 존재하는지, 존재하더라도 더 큰 집합에서 기존 집합의 주요 특성이 유지되는지는 별개의 문제이다.
Normed space가, real number와 같이, 모든 Cauchy sequence가 convergent한 경우 complete하다고 부르고 이 space를 Banach space라고 부른다.
Normed space \(V\)의 모든 Cauchy sequence가 convergent하면, \(V\)를 complete하다고 하고, Banach space라고 부른다.
'Mathematics > 선형대수' 카테고리의 다른 글
| (선형대수학) 5.4 Hilbert Projection Theorem (0) | 2018.08.03 |
|---|---|
| (선형대수학) 5.3 \(L^2\) Space (0) | 2018.08.03 |
| (선형대수학) 5.2 Hilbert Space (0) | 2018.08.03 |
| (선형대수학) 4.7 Normal Operators (0) | 2018.08.02 |
| (선형대수학) 4.6-(3) Example: Special Relativity, Lorentz Transformation (0) | 2018.08.02 |
| (선형대수학) 4.6-(2) Some Spaces Isomorphic to 3-dimensional Euclidean Space (0) | 2018.08.02 |