물리에 나오는 개념들은 수학적으로 대부분 함수입니다. 아주 기본적인 물체의 성질이라고 할 수 있는 질량, 전하량과 같은 개념들은 그냥 숫자이지만, 위치, 속도, 운동량, 힘, 전기장 등과 같은 개념들은 모두 함수로 표현됩니다. 그래서 함수가 무엇인지 잘 모르는 상태에서 물리를 시작하면 개념들과 개념들의 관계를 이해하는데 어려움을 겪게되죠.
이번 페이지에서는 함수의 일반적인 개념을 알아보고 함수와 방정식의 관계에 대하여 살펴보겠습니다.
#함수
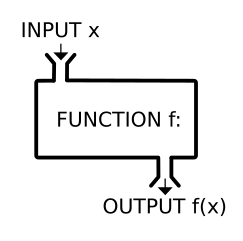
함수는 수학적으로 두 변수 사이의 관계로 설명되는데요, 간단히 말하자면 함수는 자판기 같은 기계라고 생각하면 쉽습니다.
예를 들어, 1000원을 넣으면 콜라 1캔이 나오는 자판기를 생각해봅시다.
만약 1000원짜리 지폐를 3개 넣으면 콜라가 몇 캔이 나올까요? 3캔이 나오겠죠?
6000원을 넣으면 콜라가 몇 캔이 나올까죠? 답은 6캔입니다.
이렇게 어떤 것을 넣으면, 결과로 무엇인가 나오는 기계를 함수라고 부릅니다.
By Wvbailey [Public domain], from Wikimedia Commons
하지만 이렇게 무엇을 넣으면, 결과로 어떤게 나온다고 해서 함수가 되는 것은 아니에요. 예를 들어서, 1분전에 어떤 사람이 4000원을 넣으니 콜라를 40캔을 주길래, 큰맘 먹고 4000원 넣었더니 콜라를 1캔만 주면 화나겠죠? 이 기계가 함수라고 부르려면, 입력이 똑같을 때는 반드시 그 결과가 항상 같은것이 나와야 해요. 아까전에 4000원을 넣었을 때 콜라를 40캔 줬으면, 다음사람도 4000원을 넣었을때 콜라를 40캔 줘야해요. 아, 1000원에 1캔 주는 규칙에 안맞는다고요? 그래도 만약에 그런 기계가 있다면 그 기계는 함수라고 할 수 있어요.
만약 콜라 자판기에 돌맹이를 넣었는데 콜라가 나오면 안되겠죠? 이렇게 함수에 넣을 수 있는 모든 가능성을 모아 놓은 집합을 정의역이라고 불러요. 그리고 그 결과로 나올 수 있는 모든 가능성을 모은 집합을 치역이라고 부릅니다. 만약 자판기가 1000원짜리 지폐만 받고 5000원이나 만원, 5만원 지폐는 안받는다고 하면, 정의역은
1000원짜리 지폐 1개, 1000원짜리 지폐 2개, 1000원짜리 지폐 3개, ...
가 되겠죠. 만약에 자판기가 작동하기로 약속한 1000원짜리 지폐를 넣었는데 자판기가 작동을 하지 않고 돈을 내뱉기만하면 화나겠죠? 그래서 정의역에 있는 것을 함수에 넣으면 반드시 결과값이 나와야 합니다. (물론 자판기가 0개의 캔을 주는 것도 작동 중에 하나겠죠..)
#함수의 표기
수학에서는 "돈을 넣으면 콜라가 나오는 기계"라고 부르는 대신에 문자를 사용해서 함수를 표현해요. 보통 가장많이 사용하는 문자가 함수의 영어 단어인 function의 첫글자를 따서 \(f\), 그다음 글자 \(g\), \(h\) 같은 것을 사용합니다.
예를 들어, 고등학교 수학 교과과정의 집합 단원에서 배운 밴다이어그램을 이용한 함수를 생각해 봅시다.
By Bin im Garten [CC BY-SA 3.0 ], from Wikimedia Commons
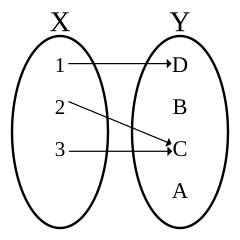
이 함수는 1을 넣으면 D가 나오고, 2를 넣으면 C, 3을 넣으면 C가 나오는 기계라는 뜻입니다. 이 함수에서 정의역은 \(\{1, 2, 3\}\)이 되고, 치역은 \(\{C, D\}\)가 되겠죠. 그리고 치역이 속해있는 전체 집합 \(\{A, B, C, D\}\)를 공역이라고 부릅니다.
수학에서 함수를 정의할 때는
$$ \mathrm{함수이름}:\mathrm{정의역이름}\to\mathrm{공역이름} $$
처럼 써서 이것이 함수라는 것을 알려줍니다.(물리에서는 잘 안쓰지만요..) 위의 함수 이름을 \(f\)라고 하고, 그림처럼 정의역을 \(X\), 공역을 \(Y\)라고 한다면,
$$ f:X \to Y $$
와 같이 \(f\)가 함수라는 것을 알려줍니다. 그리고 표현을 할 때는
$$ \mathrm{함수~}f $$
또는 미지수와 헷갈릴것을 방지하기 위해, 입력값을 미지수인 \(x\)를 이용해서
$$ f(x) $$
처럼 표현하죠. 이제 입력값을 1이라고 한다면 \(x\)대신에 1을 넣어서
$$ f(1) $$
과 같이 표현합니다. 결국 이 함수는
$$ \begin{eqnarray*} f(1)=D \\ f(2)=C \\ f(3)=C \end{eqnarray*} $$
로 압축될 수 있겠네요.
#함수와 방정식
다시 우리의 자판기로 돌아와 보죠. 우리의 콜라 자판기는 넣은 1000원짜리 지폐 갯수만큼 콜라캔을 준다는 규칙이 있었습니다. 이런 규칙을 수식으로 표현해보죠.
자판기에 넣은 1000원짜리 지폐의 갯수를 \(n\)이라고 하면, 콜라캔은 \(n\)개가 나오겠죠? 자판기 함수 이름을 \(f\)라고 한다면, 이 규칙은 수식으로
$$ f(n)=n $$
이라고 표현합니다. 만약에 옆에 자판기(함수 이름 \(g\))는 1+1 자판기라 1000원짜리 지폐 1개마다 콜라캔 2개씩 나온다면, 이 규칙은 수식으로
$$ g(n)=2n $$이 됩니다.
똑같이 규칙이 수식으로 써져 있다면 어떤 의미인지 알 수 있겠죠. 만약
$$ h(n)=n+1 $$
이라는 자판기가 있다면, 이 자판기는 1000원짜리 지폐 갯수보다 하나 더 얹어서 주는 규칙을 가지고 있을겁니다. 2000원만 가지고 있다면 1+1이나 이 자판기나 상관없지만 5000원을 가지고 있다면 1+1 자판기를 사용하겠네요.
만약 1+1 자판기에 8000원을 넣으면 몇개가 나올까요? 8000원이면 1000원짜리 지폐가 8개이니깐 \(n\) 대신에 8을 넣으면 되겠죠? 1+1 자판기 이름은 \(g\)이니깐
$$ g(8)=2\times 8 = 16 $$
콜라 16캔이 나오겠네요.
반대로 자판기 \(h\)에서 9캔을 나오게 하고싶으면 얼마를 넣어야 할까요? 이 문제는 수학적 언어로 바꾸자면
지폐가 \(n\)개 들어갔을 때, 나오는 캔의 갯수가 \(h(n)\)개일 때, \(h(n)=9\) 인 \(n\)은 몇인가?
가 됩니다. 그래서 \(h(n)=n+1=9\) 이므로 방정식
$$ n+1=9 $$
를 풀어서
$$ n=8 $$
이 됩니다. 즉, 1000원짜리 지폐 8개를 넣으면 9캔이 나온다는 뜻입니다.
자판기 \(g\)와 \(h\)가 같은 갯수의 캔을 내놓는 1000원짜리 지폐 갯수는 몇개일까요? 이 문제는
지폐가 \(n\)개 들어갔을 때, \(g(n)=g(n)\)인 \(n\)은 몇인가?
라는 문제가 됩니다. 그래서 방정식은 \(2n=n+1\)이므로
$$ n=1 $$
즉, 1000원 지폐 1개만 넣을 경우에는 자판기 \(g\)와 \(h\)가 같은 갯수의 캔(2캔)을 내놓는 다는 것을 알 수 있습니다.
#함수의 그래프
함수가 미지수에 따라서 어떻게 변화하는지 쉽게 살펴볼 수 있는 방법으로 그래프가 많이 사용됩니다. 여기에서는
$$ y=-x+5 $$
의 그래프를 그려보겠습니다.
그래프를 그리는 첫번째 작업은 정의역과 공역을 그려주는 것입니다. 일반적으로 정의역을 오른쪽으로 향하는 가로줄 화살표로, 공역을 위로 향하는 세로줄 화살표 그려줍니다. 보통 정의역의 미지수로 \(x\)를 사용하기 때문에 가로줄 화살표를 x축, 같은 이유로 세로줄 화살표를 y축이라고 부릅니다. 일반물리에서는 정의역의 미지수로 \(t\)를 사용하고 공역의 미지수로 \(x\)를 사용하는 경우가 있기 때문에, 축이름은 정의역과 공역에 사용하는 문자에 따라 그때 그때 바뀐다는 것을 주의해 주세요.
두번째 작업은 x축과 y축으로 생기는 영역의 모든 점에 이름을 붙여주는 것입니다. 일단 가로줄과 세로줄이 만나는 점을 원점이라고 부르고 수식
$$ (0,0) $$
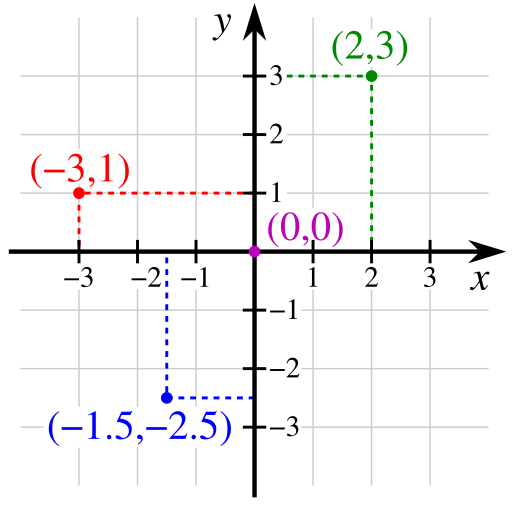
으로 표현합니다. 그리고 이 원점을 기준으로 오른쪽으로 1만큼 떨어진 지점은 첫번째 숫자를 1씩 더해서 표현합니다. 반대로 왼쪽으로 1만큼 떨어진 지점은 첫번째 숫자를 1씩 빼서 표현합니다. 위로 1만큼 이동하면 두번째 숫자를 1씩 더하고, 아래로 1만큼 이동하면 두번째 숫자를 1씩 빼서 표현합니다. 예를 들어, 원점을 기준으로 왼쪽으로 1.5, 아래로 2.5만큼 떨어진 지점을
$$ (-1.5,-2.5) $$
으로 표현합니다.
Kbolino / Public domain via Wikimedia
세번째 작업은 함수 그래프에 해당하는 점을 찍어주는 것입니다. 여러 \(x\)에 대해서 \(y\)를 구하면 다음과 같습니다.
$$ \begin{eqnarray*} x=0 \mathrm{~~이면~~} y=5 \\ x=1 \mathrm{~~이면~~} y=4 \\ x=2 \mathrm{~~이면~~} y=3 \\ x=3 \mathrm{~~이면~~} y=2 \end{eqnarray*} $$
\(x=0\) 이면 \(y=5\) 를 그래프로 표현하기 위해서 \((0,5)\) 위치에 점을 찍어줍니다. 똑같이 \(x=1\) 이면 \(y=4\)를 그래프로 표현하기 위하여 \((1,4)\) 위치에 점을 찍습니다. \(x=0.5\) , \(x=0.1111\) 일때도 각각 \(y\)가 있으므로 해당하는 \(x\)값을 첫번째 숫자에, 대응되는 \(y\)값을 두번째 숫자에 두고
$$ (x,y) $$
에 점을 찍습니다. 이렇게 찍은 점들 전체를 함수의 그래프라고 부릅니다.
이렇게 해서 함수 \(y=-x+5\) 의 그래프는 아래의 파란색 그래프와 같습니다. 빨간색 그래프는 함수 \(y=\frac{1}{2}x+2\) 의 그래프 입니다. (아래 그림은 한칸의 크기가 1)
By Jim.belk [Public domain], from Wikimedia Commons
아래의 그림은 여러 \(a\) 값에서 \(y=ax^2\) 의 그래프를 그린 것입니다.
By Ag2gaeh [CC BY-SA 4.0 ], from Wikimedia Commons
#그래프와 방정식
방정식의 해를 구하기 위해서 1.PRE 방정식과 해에서 사용한 방법을 이용할 수 있지만, 함수의 그래프를 이용할 수도 있습니다. 특히 방정식의 형태가 너무 복잡해서 직접 풀수 없는 경우에는 그래프를 이용하여 해에 관한 대략적인 정보를 얻을 수도 있습니다.
예를 들어 방정식
$$ -x+5 = \frac{1}{2}x+2 $$
를 생각해 봅시다. 만약 좌변 전체를 함수 \(f(x)\)라고 하고
$$ f(x)=-x+5 $$
우변 전체를 함수를 함수 \(g(x)\)라고 하면,
$$ g(x)=\frac{1}{2}x+2 $$
방정식의 해를 구한다는 것은
\(f(x)=g(x)\)를 만족하는 \(x\)값을 구한다
는 것과 같은 말이 됩니다. 이것을 그래프로 해석해보자면,
함수 \(f(x)\)의 그래프와 함수 \(g(x)\)의 그래프가 만나는 점의 \(x\)값을 구한다
는 것과 같은 말이 됩니다. 따라서 아래 그림에서와 같이 두 그래프는 점 \((2,3)\)에서 만나므로, 방정식 \(-x+5 = \frac{1}{2}x+2\) 의 해는 2가 됩니다. (아래 그림은 한칸의 크기가 1)
By Jim.belk [Public domain], from Wikimedia Commons
방정식이
$$ \frac{1}{2}x^2 - \frac{5}{2}x + 2 = 0 $$
처럼 방정식의 우변이 0인 경우에는, 함수 \(g(x)=0\)의 그래프가 x축이 되므로 방정식을 푼다는 것은
함수의 그래프가 x축과 만나는 점의 \(x\)값을 구하는 것
과 같습니다. 따라서 아래 그림에서 볼 수 있는 것과 같이 \(x=1\) 과 \(x=4\) 가 이 방정식의 해가 됩니다. (아래 그림은 한칸의 크기가 0.5)
By Get Learnt [CC BY-SA 4.0 ], from Wikimedia Commons
'Elementary > 일반물리' 카테고리의 다른 글
| [일반물리] 2.PRE 순간변화율 (2) | 2018.08.17 |
|---|---|
| [일반물리] 1.1 길이, 질량, 시간 단위와 단위변환 (0) | 2018.08.16 |
| [일반물리] 1.PRE 방정식과 해 (0) | 2018.08.14 |
| [일반물리] 들어가기에 앞서 (0) | 2018.08.13 |