일반물리 초반부에 사용하는 개념들은 대부분 시간의 함수로 표현됩니다. 또한 함수가 시간에 따라 얼마나 빠르게 변하는지를 알아보는 것이 일반물리의 중요한 주제입니다. 이번 페이지에서는 물리 등, 과학의 여러 분야에서 가장 많이 사용되는 변화율의 개념에 대해서 살펴보겠습니다.
#변화율
아마 우리에게 가장 익숙한 변화율의 개념은 속력일 것입니다.
100m 달리기를 하는데, A는 10초가 걸리는데, B는 20초가 걸린다면, A가 B보다 더 빠르다고 하죠. 속력은 같은 시간동안 얼마나 멀리 갈 수 있는지를 나타내는 수치입니다. 보통 1초 동안을 기준으로 얼마나 멀리 갈 수 있는지를 비교합니다. A는 10초 동안 100m를 이동했으므로 1초 동안 이동한 거리는 10m입니다. B는 20초 동안 100m를 이동했으므로 1초동안 5m를 이동했습니다. 이렇게 1초 동안 변화된 위치의 크기를 '시간에 대한 위치의 (평균)변화율'이라고 부릅니다.
$$ \mathrm{시간에~대한~위치의~변화율} = \frac{\mathrm{이동한~거리}}{\mathrm{걸린~시간}} $$
따라서 A의 변화율은
$$ \frac{\mathrm{이동한~거리}}{\mathrm{걸린~시간}} = \frac{100}{10} = 10 $$
B의 변화율은
$$ \frac{\mathrm{이동한~거리}}{\mathrm{걸린~시간}} = \frac{100}{20} = 5 $$
이 됩니다.
이를 함수 \(y(x)\)로 일반화 해봅시다. (평균)변화율은
$$ x\mathrm{에~대한~}y\mathrm{의~변화율} = \frac{y\mathrm{의~변화량}}{x\mathrm{의~변화량}} $$
으로 정의됩니다. 만약 \(x\)가 시간이고 \(y(x)\)가 위치라고 한다면, 이 정의는 위에서 정의한 것과 동일한 것임을 확인할 수 있을 것입니다.
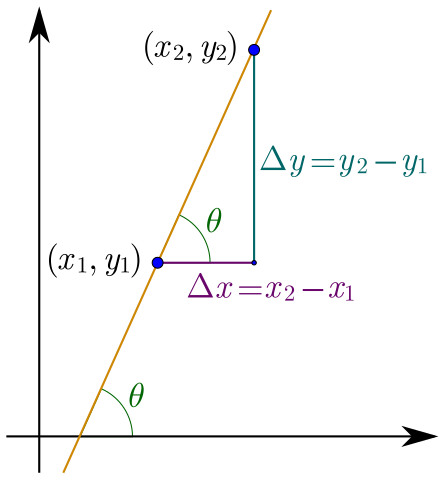
By Maschen [CC BY-SA 3.0 ], from Wikimedia Commons
위의 그래프에서 \(x\)가 \(x_1\)에서 \(x_2\)까지 변하는 동안 \(y\)는 \(y_1\)에서 \(y_2\)까지 변하므로 변화율은
$$ \mathrm{변화율} = \frac{y_2-y_1}{x_2-x_1} $$
이 됩니다. 보통 변화량을 표현할 때는 \(\Delta\) 기호('델타'라고 읽음)를 사용해서, \(x\)의 변화량은 \(\Delta x\), \(y\)의 변화량은 \(\Delta y\)로 표현합니다.
$$ \frac{\Delta y}{\Delta x} = \frac{y_2-y_1}{x_2-x_1} $$
그림에서 볼 수 있듯이, 그래프 상에서 변화율은 처음상태 \((x_1,y_1)\)과 마지막상태 \((x_2,y_2)\)를 이은 직선의 기울기임을 알 수 있습니다.
#순간변화율: 미분
위의 그림에서 \(x_2\)가 \(x_1\)에 엄청 가깝다면, 우리는 그 변화율을 \(x_1\)에서의 순간적인 변화율이라고 할 수 있을 것입니다. 이를 수학적으로 '\(x\)에대한 \(y\)의 순간변화율' 또는 '\(x\)에대한 \(y\)의 미분'이라고 부르고
$$ \frac{dy}{dx} $$
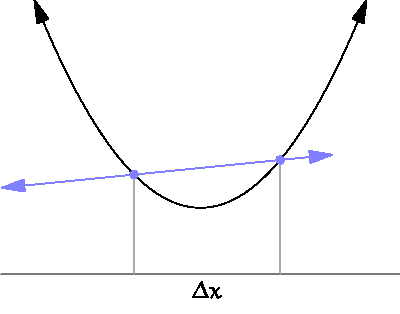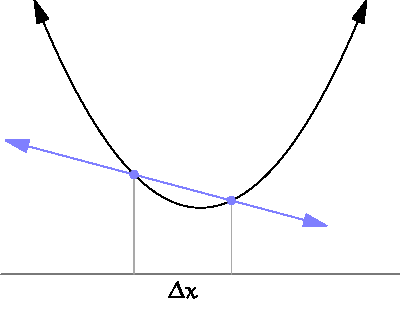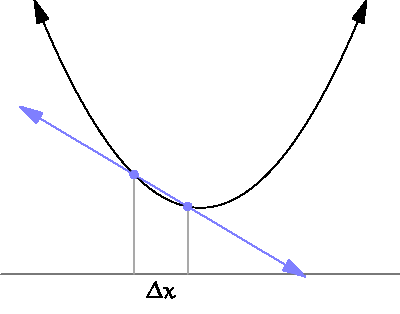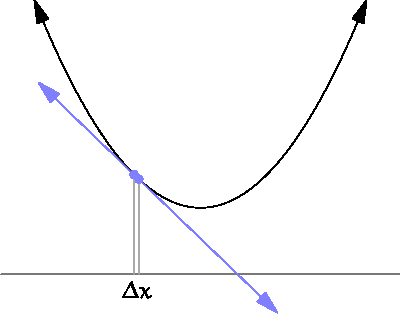
라고 씁니다. 아래 그림에서 \(\Delta x=x_2 - x_1\)이 아주 작아졌을때 파란 직선의 기울기가 순간변화율이 됩니다.1
By Brnbrnz [CC BY-SA 4.0 ], from Wikimedia Commons
- 미분에 대한 자세한 것은 --calculus,derivative-- 참고. [본문으로]
'Elementary > 일반물리' 카테고리의 다른 글
| [일반물리] 1.1 길이, 질량, 시간 단위와 단위변환 (0) | 2018.08.16 |
|---|---|
| [일반물리] 1.PRE 함수와 방정식 (0) | 2018.08.14 |
| [일반물리] 1.PRE 방정식과 해 (0) | 2018.08.14 |
| [일반물리] 들어가기에 앞서 (0) | 2018.08.13 |