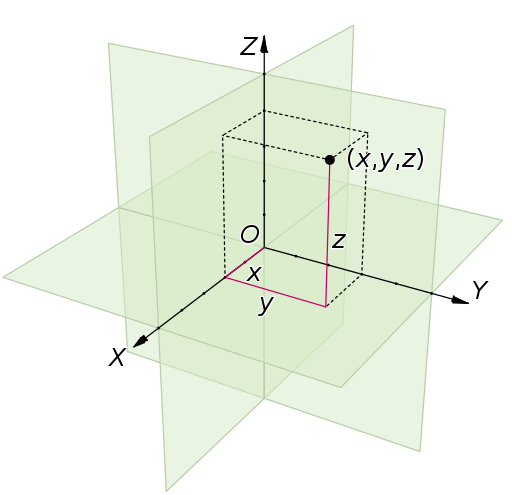
3차원 Euclidean space에 있는 surface \(S\)에 대하여 vector field \(\mathbf{F}\)의 surface integration은 surface의 normal vector \(\mathbf{n}_1\)을 이용하여
$$ \iint _S \mathbf{F} \cdot \mathbf{n}_1 ~d\Sigma $$
으로 정의한다. 그러나 surface의 normal vector를 잡는 방법은 두가지가 있다.
See page for author [Public domain], via Wikimedia Commons
만약 normal vector를 \(\mathbf{n}_1\) 대신 \(\mathbf{n}_2\)를 이용하면,
$$ \mathbf{n}_2 = -\mathbf{n}_1 $$
이므로 surface integration의 결과값은 부호가 반대가 될것이다.
$$ \iint _S \mathbf{F} \cdot \mathbf{n}_2 ~d\Sigma = -\iint _S \mathbf{F} \cdot \mathbf{n}_1 ~d\Sigma $$
따라서 surface integration을 하기 이전에 surface의 normal vector 방향을 결정해야 하는데, 이는 surface에 정의된 좌표축으로부터 결정한다.
2차원인 surface에 좌표축을 아래 그림의 왼쪽처럼 잡으면 오른손 법칙에 의해 normal vector는 \(\mathbf{n}_2\)가 되고 오른쪽처럼 잡으면 \(\mathbf{n}_1\)으로 정의한다. 좌표축을 정렬하는 방법에 따라 surface의 normal vector가 결정된다. 이렇게 좌표축을 정렬하는 방법을 orientation이라고 한다.
Orientations on Vector spaces
선형대수학 정리에 따르면, \(n\)-dimensional vector space \(V\)의 2개의 ordered basis
$$ \mathcal{B} = \{ \mathbf{e}_1 , \mathbf{e}_2 , \cdots, \mathbf{e}_n \} $$
$$ \mathcal{B}' = \{ \mathbf{e}' _1, \mathbf{e}' _2, \cdots, \mathbf{e}' _n \} $$
에 대하여
$$ A(\mathbf{e}_i) = \mathbf{e}' _i $$
를 만족하는 isomorphism \(A\)가 존재한다. 만약 \(A\)가
$$ \det{A} > 0 $$
이면 ordered basis \(\mathcal{B}\)와 \(\mathcal{B}'\)이 서로 같은 orientation을 갖는다고 부른다. 반대로
$$ \det{A} < 0 $$
이면 ordered basis \(\mathcal{B}\)와 \(\mathcal{B}'\)은 서로 반대의 orientation을 갖는다고 부른다. (\(A\)는 invertible이므로 \(\det{A} \ne 0\)이다.) 따라서 ordered basis는 2가지 종류의 orientation으로 분류되는데 그중 하나를 \(+1\) 다른 하나를 \(-1\)로 표현하기도 한다.
Example: 3-dimensional Euclidean Space
일반적으로 3차원 Euclidean space는 standard ordered basis를 orientation \(+1\)로 정의한다.
By Jorge Stolfi [Public domain], from Wikimedia Commons
이제 standard ordered basis에 다음과 같은 linear operator \(A_1\)를 작용하여 얻어지는 ordered basis를 생각해보자.
$$ A_1 = \left( \begin{array}{ccc} \cos{\theta} & -\sin{\theta} & 0 \\ \sin{\theta} & \cos{\theta} & 0 \\ 0 & 0 & 1 \end{array} \right) $$
\(A_1\)의 determinant는 1이므로 이 좌표축의 orientation도 \(+1\)이다. 그림에서 보는바와 같이 이 좌표축은 일반적인 좌표축을 z축으로 회전한 좌표축이므로 오른손 법칙을 따른다는 것을 알 수 있다.
By JohnBlackburne [CC BY-SA 3.0 or GFDL], from Wikimedia Commons
이제 다음과 같은 linear operator \(A_2\)를 작용하여 얻어지는 ordered basis를 생각해보자.
$$ A_2 = \left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array} \right) $$
\(A_2\)의 determinant는 -1이므로 이 좌표축의 orientation은 \(-1\)이다. 그림에서 보는바와 같이 이 좌표축은 일반적인 좌표축에서 x축과 y축을 바꾼 좌표축으로 왼손 법칙을 따른다.
\(A_1\)과 같이 determinant가 양수인 linear operator를 orientation-preserving하다고 부른다.
Orientability of Differentiable Manifold
Differentiable manifold \(M\)의 point \(p\)가 parameterization \((U,x)\) 와 \((V,y)\) 에 동시에 속한다면, tangent space \(T_pM\)에 대한 \(x\)에서의 ordered basis
$$ \mathcal{B} = \left\{ \frac{\partial}{\partial x^1} , \frac{\partial}{\partial x^2} ,\cdots, \frac{\partial}{\partial x^n} \right\} $$
는 transition function의 differential(local coordinate 표현으로는 Jacobian matrix, 1.3 Tangent Space, Tangent Bundle 참고)에 의하여 ordered basis
$$ \mathcal{B}' = \left\{ \frac{\partial}{\partial y^1}, \frac{\partial}{\partial y^2}, \cdots, \frac{\partial}{\partial y^n} \right\} $$
가 얻어진다. 따라서 Jacobian determinant가 양수인 경우 transition function을 orientation-preserving하다고 부른다. 만약 atlas의 모든 transition function이 orientation-preserving한 경우 oriented atlas라고 부른다.
DEFINITION Orientability of Differentiable Manifold
Differentiable manifold \(M\)이 oriented atlas를 가지는 경우 \(M\)을 orientable하다고 부른다.
다음 그림의 surface는 orientable하며, 두가지 가능한 orientation 중 오른손 법칙을 선택하여 normal vector를 표현한 그림이다.
By Lucas V. Barbosa [Public domain], from Wikimedia Commons
대표적인 non-oreintable manifold는 Möbius strip이다. 다음 그림에서 보는 바와 같이 게의 집게을 오른쪽에 두고 한바퀴 돌리면 게의 집게가 왼쪽으로 바뀌고 반대로 게의 집게가 왼쪽에서 시작하면 오른쪽으로 바뀐다. 이는 orientation을 manifold 전체에 맞도록 설정해 줄 수 없다는 뜻이다.
By Hamishtodd1 [CC BY-SA 4.0 ], from Wikimedia Commons
'Mathematics > 다양체(텐서)' 카테고리의 다른 글
| [다양체,텐서] 2.3 Tensor Fields (0) | 2018.09.08 |
|---|---|
| [다양체,텐서] 2.2 Symmertric Tensors, Antisymmetric Tensors, Exterior Algebra (0) | 2018.09.08 |
| [다양체,텐서] 2.1 Tensor Product (2) | 2018.09.08 |
| [다양체,텐서] 1.7 Submanifold (0) | 2018.08.18 |
| [다양체, 텐서] 1.6 Integral Curve (0) | 2018.08.18 |
| [다양체,텐서] 1.5 Vector Fields, Lie Bracket (3) | 2018.08.12 |