열평형 상태의 macrostate이더라도 입자의 위치나 운동량 등은 시시각각 변하는 것처럼 microstate는 시간에 따라 변하고 있다. 그래서 실험적으로 어떤 물리값을 측정한다는 것은 시간에 따라서 변하는 microstate에 대한 물리값의 평균값이 얻어진다고 할 수 있을 것이다. 이와 비슷하게 시간의 평균값 대신, 수많은 동일한 macrostate(그러나 다른 microstate)의 복사본에 대해서 평균값을 얻는 것도 같은 효과를 보일 것이라고 할 수 있다. 이렇게 macrostate의 복사본을 모아놓은 세트를 ensemble(앙상블)이라고 부른다.
이번 페이지에서는 ensemble 이론의 기초를 살펴본다.
#Phase Space
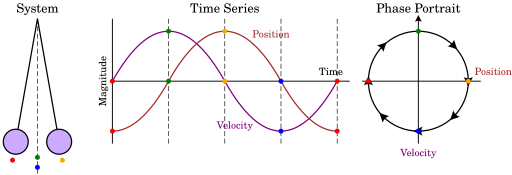
고전역학에서 특정 시간에 한 시스템을 표현하는 것은 position와 momentum으로 표현되는 phase space1 상의 한 점으로 나타난다. 예를 들어, 입자 1개가 1차원 공간에서 움직이는 시스템은 position \(x\) 와 momentum \(p\) 로 구성된 공간의 한 점으로 나타난다. 아래 그림은 진자의 운동을 phase space에서 나타낸 그림이다. 진자(맨 왼쪽)는 빨강 → 초록 → 노랑 → 파랑 → 빨강 으로 운동을 한다. 초록과 파랑의 위치는 같지만, 속도가 반대임을 주의하자. 이 사실은 시간에 대한 위치 속력 그래프(중앙)에서 확인할 수 있다. 이 때 각 점의 위치와 속력(또는 운동량)을 각각 x축, y축으로 배치하면 phase space(맨 오른쪽)가 된다.
Krishnavedala / CC BY-SA via Wikimedia
\(N\) 개의 입자가 3차원 공간에서 움직이는 시스템은 position \(x_1\) , \(x_2\) , ... , \(x_{3N}\) 과 momentum \(p_1\) , \(p_2\) , ... , \(p_{3N}\) 의 6N-차원 phase space \(\mathbb{R}^{6N}\) 상의 한 점으로 표현된다. 이 점은 시간에 따라 Hamilton's equation을 따라 움직이게 된다.2
\[ \begin{align*} \dot{x}_i &= \frac{\partial H}{\partial p_i} \\ \\ \dot{p}_i &= -\frac{\partial H}{\partial x_i} \end{align*} \]
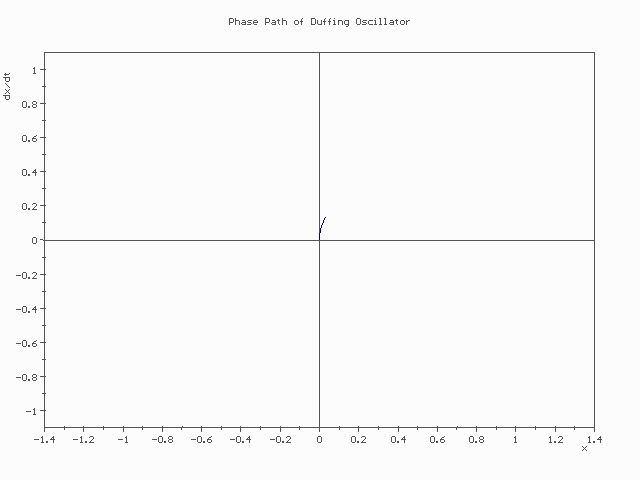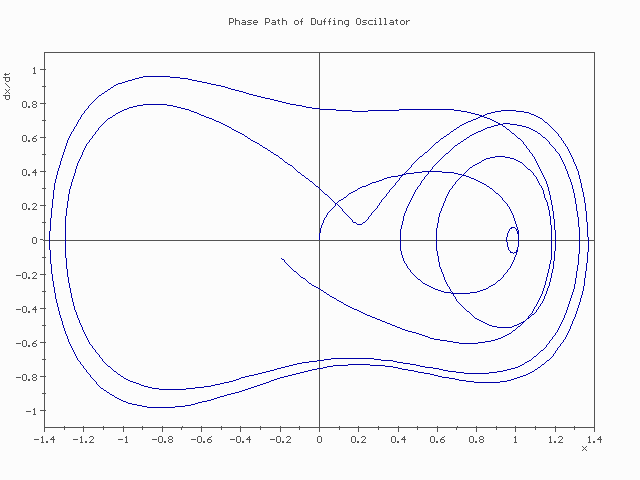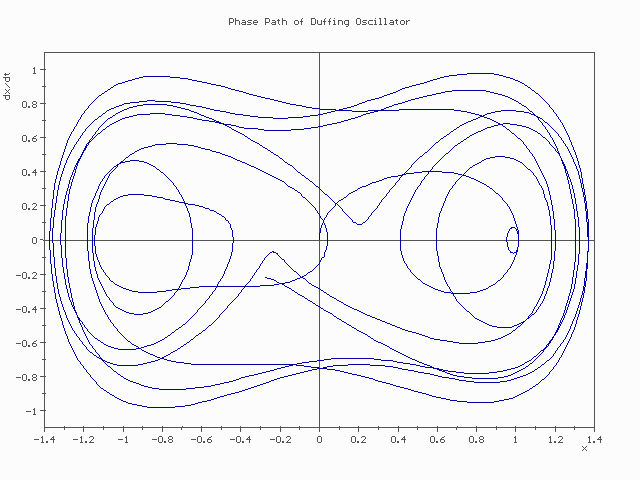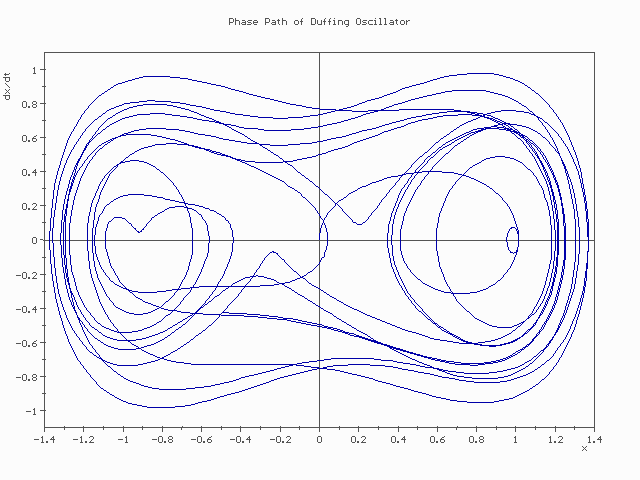
따라서 시스템이 시간에 따라 변하는 것은 phase space 상의 curve로 나타나며, 이 curve의 tangent vector3 \(\mathbf{v} = (\dot{x}_i,\dot{p}_i)\) 가 바로 Hamilton's equation에 의하여 결정된다. 다음 그림은 Duffing oscillator라는 시스템이 phase space 상에서 어떻게 이동하는지를 보여주는 그림이다. 끝점이 이동하는 방향과 속력은 Duffing oscillator의 Hamilton's equation에 의하여 결정된다.
Pasimi / CC BY-SA via Wikimedia
#Density Function
주어진 macrostate에 대하여 서로 다른 microstate들은 phase space 상에서 다른점으로 나타나게 된다. 다음 그림에서, 색칠된 영역을 phase space 상에서 주어진 macrostate가 되는 점들을 모두 모아놓은 집합이라면, 각 microstate들은 다른 점들에 대응이 된다.
주어진 Macrostate의 ensemble은 주어진 macrostate에 들어있는 모든 점4들에 해당하는 시스템을 적당한 개수씩 복사하여 구성한다. 이 때, phase space의 점 \((x,p)\)에 해당하는 microstate가, phase space에 복제된 개수를 density function이라고 한다. 보통은 phase space 상의 점들은 연속적이기 때문에, 각 점마다 density function \(\rho(x,p,t)\) 를 부여하여 ensemble을 구성한다.
\(\rho(x,p,t)\)의 의미는, 시간 \(t\) 일 때 ensemble 안에, \((x,p)\) 의 주변 \(d^{3N}x d^{3N}p\) 부피 안에 들어 있는 microstate의 개수가 \(\rho(x,p,t) ~d^{3N}x~d^{3N}p\) 가 있다는 뜻이다.5 6
#Liouville's Theorem
\(\rho\) 가 어떤 부피 \(\omega\) 에 갇혀있다고 하자.7 이 부피에서 \(\rho\) 가 변하는 양은
\[ \frac{\partial}{\partial t} \int _\omega \rho ~d\omega \]
가 된다. 또한 \(\rho\)가 이 부피의 경계 \(\partial \omega\)를 빠져나가는 flux8는 divergence theorem에 의해
\[ \int _{\partial \omega} \rho \mathbf{v} \cdot d\mathbf{a} = \int _\omega \mathrm{div}(\rho\mathbf{v}) ~d\omega \]
이다. 개념상으로 \(\rho\) 가 \(\omega\) 에서 변하는 양은 들어오는 flux와 같아야 하므로
\[ \frac{\partial}{\partial t} \int _\omega \rho ~d\omega = -\int _\omega \mathrm{div}(\rho\mathbf{v}) ~d\omega \]
따라서
\[ \int _\omega \frac{\partial \rho}{\partial t} + \mathrm{div}(\rho\mathbf{v}) ~d\omega = 0 \]
이 때, \(\omega\) 는 임의로 잡은 것이므로 모든 \(\omega\) 에 대해서 성립하기 위해서는
\[ \frac{\partial \rho}{\partial t} + \mathrm{div}(\rho\mathbf{v}) = 0 \]
이어야 한다. Divergence를 계산하면,
\[ \begin{align*} \mathrm{div}(\rho\mathbf{v}) &= \sum_{i=1} ^{3N} \frac{\partial}{\partial x_i} (\rho \dot{x}_i) + \frac{\partial}{\partial p_i} (\rho \dot{p}_i) \\ &= \sum_{i=1} ^{3N} \frac{\partial\rho}{\partial x_i} \dot{x}_i + \rho \frac{\partial\dot{x}_i}{\partial x_i} + \frac{\partial \rho}{\partial p_i} \dot{p}_i + \rho \frac{\partial \dot{p}_i}{\partial p_i} \end{align*} \]
여기에 Hamilton's equation을 대입하자.9
\[ \begin{align*} \mathrm{div}(\rho\mathbf{v}) &= \sum_{i=1} ^{3N} \frac{\partial\rho}{\partial x_i} \frac{\partial H}{\partial p_i} + \rho \frac{\partial^2 H}{\partial x_i \partial p_i} - \frac{\partial \rho}{\partial p_i} \frac{\partial H}{\partial x_i} - \rho \frac{\partial^2 H}{\partial p_i \partial x_i} \\ &= \sum_{i=1} ^{3N} \frac{\partial\rho}{\partial x_i} \frac{\partial H}{\partial p_i} - \frac{\partial \rho}{\partial p_i} \frac{\partial H}{\partial x_i} \\ &= \left\{ \rho, H \right\} \end{align*} \]
따라서
\[ \frac{\partial \rho}{\partial t} + \left\{ \rho, H \right\} = 0 \]
이 식을 Liouville's theorem(리우빌 정리)이라고 한다. 위 식의 좌변은 \(\frac{d\rho}{dt}\) 이다.10 따라서 Liouville's theorem의 의미는 \(\rho\) 가 시간이 지나면서 움직이지만 총 밀도는 변하지 않는다는 뜻이다. 마치 액체가 흘러가듯이 밀도가 없어지거나 새로 생기지 않고 \(\rho\) 가 이동한다. 아래 그림을 이 관점에서 잘 생각해보자. 각 점은 phase space 상의 microstate를 표현한다. 각 점들은 Hamilton's equation을 따라 이동하는데(예를 들어 빨간색 점과 녹색 점의 움직임), 시스템의 흐름에 의해 고정된 점에서 \(\rho\) 의 값들은 변하지만 총 밀도는 늘어나지도 줄어들지도 않는다.
Nanite / CC0 via Wikimedia
#Microcanonical Ensemble #Canonical Ensemble
Density function \(\rho\) 가 시간에 대하여 explicit하게 표현되지 되는 경우, 즉 \(\frac{\partial \rho}{\partial t} = 0\) 인 경우 ensemble이 stationary하다고 부른다. 즉, 위의 그림과는 다르게 \(\rho\)가 움직이지 않을 때, ensemble이 stationary하다고 한다. Stationary의 대표적인 예가 equilibrium 상태이다. 따라서 equilibrium 상태에 있는 시스템의 ensemble은 density function이 Liouville's theorem과 stationary 조건을 모두 만족하도록, phase space 상의 각 점이 표현하는 microstate들의 개수를 선택해야 한다. 즉,
\[ \left\{ \rho , H \right\} = 0 \]
를 만족해야 한다.
이를 만족하는 \(\rho\) 중에 하나는
\[ \rho(x,p) = \text{상수} \]
가 있다. 즉, ensemble을 구성할 때, 주어진 macrostate에 허용되는 모든 microstate가 ensemble 내에 동일한 비율로 존재하도록 구성한 것과 같다. 이러한 density function로 구성된 ensemble을 microcanonical ensemble(소정준 앙상블)이라고 한다. equal a priori probabilities를 이용하여 1.1-(1) Example: 이상 기체, 기브스 역설 Ideal Gas, Gibbs Paradox에서 구한 방식이 microcanonical ensemble이다.
또 다른 가능성으로
\[ \rho(x,p) = \exp{(-\frac{H}{kT})} \]
도 위 식을 만족한다. 이러한 density function으로 구성된 ensemble을 canonical ensemble(정준 앙상블)이라고 한다.11
#Ensemble Average
위의 내용들을 정리하면 Density function \(\rho\) 는 probability density function(확률 밀도 함수)의 역할을 한다. 즉, 시스템이 주어진 macrostate에 대하여 microstate \((x,p)\) 의 주변 \(d^{3N}xd^{3N}p\) 부피 안에 들어있을 확률이 \(\rho(x,p)~d^{3N}xd^{3N}p\) 에 비례한다.
\[P(x,p) ~d^{3N}x d^{3N}p ~~~\propto~~~ \rho(x,p)~d^{3N}xd^{3N}p\]
확률의 총합이 1이 되어야 하므로 \(\rho\) 의 적분값으로 나누어 다음 식을 얻는다.
THEOREM Probability of System in Microstate
Equilibrium 상태에 있는 시스템의 density function을 \(\rho\) 라고 하면, 시스템이 microstate \((x,p)\) 의 주변 \(d^{3N}xd^{3N}p\) 부피 안에 들어있을 확률은 다음과 같다.
\[ P(x,p) ~d^{3N}x d^{3N}p = \frac{ \rho(x,p)~d^{3N}xd^{3N}p}{\int \rho(x,p)~d^{3N}xd^{3N}p} \]
만약 quantum state 같이 허용된 microstate가 불연속적이라면, \(\rho\) 는 probability mass function(확률 질량 함수)가 되고, 분모의 적분은 합으로 바뀐다.
이제, 시스템의 물리량 \(f\) 를 측정한다고 하자. 현실적으로 \(f\) 를 측정한다는 것은 특정한 순간이 아닌, 원자나 분자 입자에서는 긴 시간 동안 측정된 측정하는 것이라고 할 수있다. 그 시간 동안, 시스템의 microstate는 변하기 때문에, 물리량 \(f\) 의 값도 변할 것이다. 따라서 \(f\) 의 측정값은 긴 시간동안의 평균값이다. 이 때, equilibium 상태에서는 microstate가 위의 확률 분포를 따르므로, 긴 시간동안 각 microstate에 머무르는 시간의 비율 역시 확률 분포를 따른다고 할 수 있다. 따라서 열역학적으로 \(f\) 를 측정하는 것은 위에서 정의한 확률 분포에서 \(f\) 가 가지는 expected value(기대값)12이라고 할 수 있다. 이 값을 \(f\) 의 ensemble average라고 한다.
DEFINITION Ensemble Average
Equilibrium 상태에 있는 시스템의 density function을 \(\rho\) 라고 하면, 물리량 \(f\) 의 ensemble average를 다음과 같이 정의한다.
\[ \langle f \rangle = \frac{ \int f(x,p) \rho(x,p)~d^{3N}xd^{3N}p}{\int \rho(x,p)~d^{3N}xd^{3N}p} \]
위의 확률과 마찬가지로 microstate가 불연속적이라면, 우변의 적분은 합으로 바꿔서 정의한다.
- --classical,phasespace-- 참고. [본문으로]
- \\(H\\) 는 이 시스템의 Hamiltonian이다. [본문으로]
- curve의 tangent vector는 --calculus,tangent vector of curve-- 참고. Manifold에서는 [다양체,텐서] 1.3 Tangent Space, Tangent Bundle 참고. [본문으로]
- 위 그림에서는 색칠된 영역. [본문으로]
- 위 그림은 간단한 이해를 위해서 phase space 상의 점들이 불연속인 경우처럼 취급했다. 연속인 경우 microstate의 경우의 수가 무한대가 되기 때문에 개수를 하나하나 세는 것은 의미가 없고 본문처럼 해석해야 한다. [본문으로]
- 사실상 density function은 시스템이 \\((x,p)\\)에 있을 확률을 나타내는 확률밀도함수의 일종이다. 확률밀도함수의 자세한 내용은 [통계학] 1.6 확률 질량 함수, 확률 밀도 함수 Probability Mass Function, Probability Density Function 참고. [본문으로]
- 위 그림에서는 색칠된 영역이다. [본문으로]
- 시스템 curve의 tangent \\(\\mathbf{v}\\) 와 경계 벡터 \\(d\\mathbf{a}\\) 의 내적값에 밀도 \\(\\rho\\)를 곱한 값이어야 한다. [본문으로]
- 마지막 줄은 Poisson bracket이다. Poisson bracket에 대한 내용은 --classical,poissonbracket-- 참고. [본문으로]
- --classical,Hamilton's euation-- 참고. [본문으로]
- canonical ensemble에 대한 내용은 1.4 정준 앙상블 Canonical Ensemble에서 다룬다. [본문으로]
- 확률론의 expected value 내용은 [통계학] 2.2 기대값 Expected Values 참고. [본문으로]
'Physics > 통계역학' 카테고리의 다른 글
| [통계역학] 1.4-(1) Example: 정준 앙상블에서 열역학적 물리량 Thermodynamic Quantities in Canonical Ensemble (0) | 2020.08.06 |
|---|---|
| [통계역학] 1.4 정준 앙상블 Canonical Ensemble (3) | 2020.08.04 |
| [통계역학] 1.3 소정준 앙상블 Microcanonical Ensemble (2) | 2020.08.01 |
| [통계역학] 1.1-(1) Example: 이상 기체, 기브스 역설 Ideal Gas, Gibbs Paradox (5) | 2020.07.28 |
| [통계역학] 1.1 거시상태, 미시상태, 볼츠만 상수 Macrostate, Microstate, Boltzmann Constant (4) | 2020.07.28 |
| [통계역학] PRE. 열역학 Thermodynamic Introduction (1) | 2020.07.27 |