(선형대수학) 4.3 Orthogonality, Gram-Schmidt Process

공간벡터의 내적과 길이, 각도의 관계

$$\overrightarrow{x}\cdot \overrightarrow{y}=\left|\overrightarrow{x}\right|\left|\overrightarrow{y}\right|\cos \theta$$

로부터 inner product space에서 두 vector 사이의 각도를 정의할 수 있다.

$$\theta ={\cos }^{-1}\frac{⟨\mathbf{x},\mathbf{y}⟩}{\sqrt{⟨\mathbf{x},\mathbf{x}⟩}\sqrt{⟨\mathbf{y},\mathbf{y}⟩}}$$

공간벡터의 내적에서 두 공간 벡터 사이의 각도가 $\frac{\pi }{2}$(직각)인 경우 내적은 0이 되는데, 많은 계산에서 계산이 간단해지므로 좋은 도구가 된다. Inner product에서도 이에 대응되는 개념을 다음과 같이 정의한다.

 

DEFINITION            Orthogonality

 

Inner product space $V$의 vector $\mathbf{x}$와 $\mathbf{y}$가

$$⟨\mathbf{x},\mathbf{y}⟩=0$$

이면 $\mathbf{x}$와 $\mathbf{y}$는 orthogonal하다 고 부른다. Vector들의 집합 $A$에 대하여 임의의 vector $\mathbf{x}\in A$와 $\mathbf{y}\in A$가 항상 orthogonal한 경우 집합 $A$를 orthogonal set이라고 부른다. 만약 orthogonal set $A$의 모든 vector들이

$$⟨\mathbf{x},\mathbf{x}⟩=1$$

즉, norm이 1인 경우 집합 $A$를 orthonormal set이라고 부른다.

 

경우에 따라 두 vector들의 집합 $A$와 $B$가 서로 orthogonal하다는 표현을 쓰기도 하는데, 이는 임의의 vector $\mathbf{x}\in A$와 $\mathbf{y}\in B$가 항상 orthogonal하다는 것으로 이해하면 된다.

 

Inner product의 basis가 $\{{\mathbf{e}}_i\}$인 경우

$$\mathbf{x}=\sum _i{x}_i{\mathbf{e}}_i$$

$$\mathbf{y}=\sum _j{y}_j{\mathbf{e}}_j$$

의 inner product는 inner product의 linearity로부터

$$⟨\mathbf{x},\mathbf{y}⟩=\sum _{i,j}{x}_i{\bar{y}}_j⟨{\mathbf{e}}_i,{\mathbf{e}}_j⟩$$

가 된다. 만약 basis vector들 사이에

$$⟨{\mathbf{e}}_i,{\mathbf{e}}_j⟩=0\mathrm{for}i\ne j$$

의 관계가 있다면

$$⟨\mathbf{x},\mathbf{y}⟩=\sum _i{x}_i{\bar{y}}_i⟨{\mathbf{e}}_i,{\mathbf{e}}_i⟩$$

로 inner product가 간단해진다. 여기에

$$⟨{\mathbf{e}}_i,{\mathbf{e}}_i⟩=1$$

의 관계가 성립한다면

$$⟨\mathbf{x},\mathbf{y}⟩=\sum _i{x}_i{\bar{y}}_i$$

가 된다. 즉, Basis를 orthonormal set으로 택하는 것은 inner product를 계산을 간단하게 해준다.

이러한 basis를 orthonormal basis라고 부른다.

 

DEFINITION            Orthonormal Basis

 

Vector space $V$의 basis $\mathcal{B}$가 모든 $i$, $j$에 대하여 basis vector ${\mathbf{e}}_i$, ${\mathbf{e}}_j\in \mathcal{B}$가

$$⟨{\mathbf{e}}_i,{\mathbf{e}}_j⟩={\delta }_{ij}$$

인 경우, 즉, $\mathcal{B}$가 orthonormal set인 경우 $\mathcal{B}$를 orthonormal basis라고 부른다.

 

예를 들어, Euclidean space ${\mathbb{C}}^n$의 standard basis

$${\mathbf{e}}_i=(0,\cdots ,0,1,0,\cdots ,0)$$

은 stamdard inner product에서 orthonormal basis이다. Orthogonality는 inner product로부터 정의되므로 inner procuct가 달라지면 orthogonality도 달라진다. Orthonormal basis의 경우 vector를 basis로 전개했을 때 $(i$)번째 계수를 inner product로부터 쉽게 표현할 수 있다.

$$x_i=⟨\mathbf{x},{\mathbf{e}}_i⟩$$

 

 

Gram-Schmidt Process

 

문제는 임의의 inner product space에서 언제나 orthonormal basis를 찾을 수 있는가 이다. 일단, Finite-dimensional inner product space의 경우 언제나 orthonormal basis를 찾을 수 있다. 하나의 basis로부터 새롭게 orthonormal basis를 얻어내는 방법 중 하나가 Gram-Schmidt process이다. Gram-Schmidt process의 핵심은 linearly independent한 두 vector $\mathbf{x}$와 $\mathbf{y}$으로 얻을 수 있는 vector

$$\mathbf{y}-\frac{⟨\mathbf{x},\mathbf{y}⟩}{⟨\mathbf{x},\mathbf{x}⟩}\mathbf{x}$$

는 $\mathbf{x}$와 linearly independent하고

$$⟨\mathbf{x},\mathbf{y}-\frac{⟨\mathbf{x},\mathbf{y}⟩}{⟨\mathbf{x},\mathbf{x}⟩}\mathbf{x}⟩=0$$

즉, $\mathbf{x}$와 orthogonal 하다는 것이다.이를 이용하여 orthonormal하지 않은 basis

$$\mathcal{B}=\{{\mathbf{e}}_1,{\mathbf{e}}_2,\cdots ,{\mathbf{e}}_n\}$$

에서

 

1. 첫 번째 vector를 아무 것이나 택한다.

$${\mathbf{f}}_1={\mathbf{e}}_1$$

 

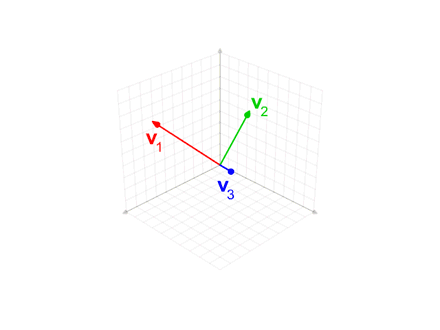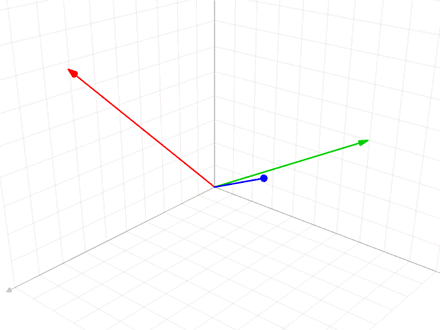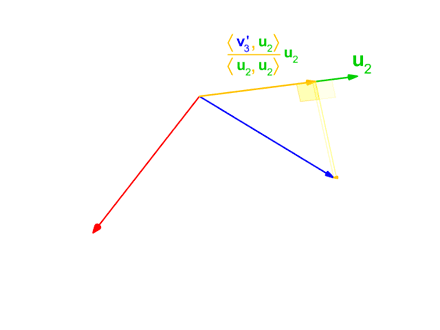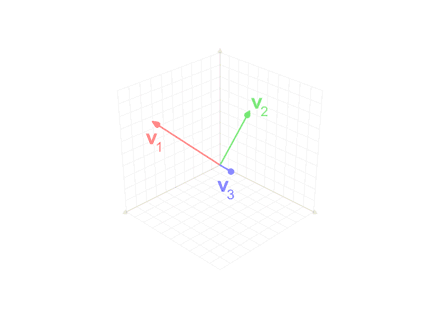
2. 두 번째 vector를 선택하여 첫 번째와 linearly independent하고 orthogonal한 새로운 vector를 얻는다.

$${\mathbf{f}}_2={\mathbf{e}}_2-\frac{⟨{\mathbf{f}}_1,{\mathbf{e}}_2⟩}{⟨{\mathbf{f}}_1,{\mathbf{f}}_1⟩}{\mathbf{f}}_1$$

 

3. 세 번째 벡터를 선택하여 첫 번째와 linearly independent하고 orthogonagl한 새로운 vector를 얻고 이를 이용해 다시 두 번째 vector와 linearly independent하고 orthogonal한 새로운 vector를 얻는다.

 

4. 이를 $n$번째 vector까지 반복한다.

 

5. 새로 얻은 $n$개의 vector의 norm을 1로 만들어 준다.

$${\mathbf{g}}_i=\frac{{\mathbf{f}}_i}{\sqrt{⟨{\mathbf{f}}_i,{\mathbf{f}}_i⟩}}$$

 

이렇게 얻은 새로운 basis

$$\mathcal{C}=\{{\mathbf{g}}_1,{\mathbf{g}}_2,\cdots ,{\mathbf{g}}_n\}$$

은 orthonormal set이다.

 

By Lucas V. Barbosa [Public domain], from Wikimedia Commons

 

 

 

Orthogonal Complement of Subspace

 

${\mathbb{R}}^3$의 subspace인 xy-plane

$$S=\{(x,y,0)|x,y\in \mathbb{R}\}$$

에 대하여, 또다른 subspace인 z-axis

$$P=\{(0,0,z)|z\in \mathbb{R}\}$$

는 서로 직각이다.

 

By Jorge Stolfi [Public domain], from Wikimedia Commons

 

$S$와 $P$는 서로 직각이기 때문에 그들의 vector 역시 직각이다. 즉, vector $\overrightarrow{v}\in S$, $\overrightarrow{w}\in P$가

$$\overrightarrow{v}\cdot \overrightarrow{w}=0$$

이다. 또한 $S+P={\mathbb{R}}^3$이고, $S\cap P=\{(0,0,0)\}$이므로

$${\mathbb{R}}^3=S\oplus P$$

이다. 이렇게 subspace와 직각인 나머지 모든 부분을 모은 집합을 일반화하여 orthogonal complement라고 한다.

 

DEFINITION            Orthogonal Complement

 

Inner product space $V$의 subspace $W$에 대하여, 집합

$$W^{\perp }=\{\mathbf{v}\in V|⟨\mathbf{v},\mathbf{w}⟩=0\mathrm{for}\mathrm{all}\mathbf{w}\in W\}$$

를 $W$의 orthogonal Complement라고 한다.

 

3-dimensional Euclidean space와 같이, Subspace $W$와 $W^{\perp }$는 $V$의 direct sum이 된다.

 

THEOREM            

 

Inner product space $V$와 $V$의 subspace $W$에 대하여,

$$V=W\oplus W^{\perp }$$

 

${\mathbb{R}}^3$의 예제의 경우

$${\left(S^{\perp }\right)}^{\perp }=P^{\perp }=S$$

가 된다. 일반적으로 finite dimensional inner product space의 경우

$${\left(W^{\perp }\right)}^{\perp }=W$$

가 성립한다. 그러나 infinite dimensional inner product space의 경우 ${\left(W^{\perp }\right)}^{\perp }\ne W$일 수 있다.