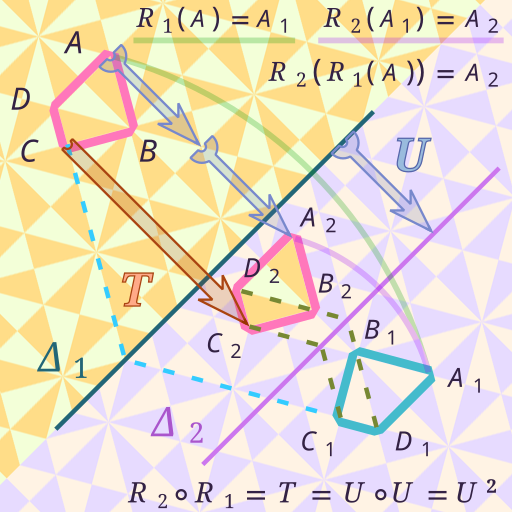
Isomorphism은 vector space \(V\)와 \(W\)가 vector의 기본 연산인 vector addition과 scalar multiplication의 결과가 그대로 유지되도록 연결시켜주는 linear transformation이다. \(T\)가 \(V\)에서 \(W\)로의 isomorphism이라고 하면, 모든 \(V\)의 vector \(\mathbf{v}_1\), \(\mathbf{v}_2\)와 scalar \(c\)에 대하여
$$ T(\mathbf{v}_1+\mathbf{v}_2)=T\mathbf{v}_1+T\mathbf{v}_2 $$
$$ T(c\mathbf{v}_1)=c(T\mathbf{v}_1) $$
즉, \(T\)로 변환 전 \(V\)에서의 연산과 변환 후의 (\(W\)에서의) 연산이 동일하다.
새로운 vector들의 연산인 inner product에 대해서도 비슷한 개념을 생각할 수 있다. Inner product space \(V\)(inner product는 \(\left\langle \cdot , \cdot \right\rangle _V\)로 표시하자. 이하에서 space를 구별할 필요가 없을때는 생략한다)와 \(W\)에 대하여 linear transformation \(T:V\to W\)가 모든 \(V\)의 vector \(\mathbf{v}_1\), \(\mathbf{v}_2\)에 대하여
$$ \left\langle \mathbf{v}_1 , \mathbf{v}_2 \right\rangle _V = \left\langle T\mathbf{v}_1 , T\mathbf{v}_2 \right\rangle _W $$
즉, \(T\)로 변환 전의 (\(V\)에서의) inner product와 변환 후의 (\(W\)에서의) inner product가 동일한 경우 \(T\)가 inner product를 보존한다(preserve)고 하고 \(T\)를 isometry라고 부른다.
Inner product space \(V\)와 \(W\)에 대하여, 함수 \(f:V \to W\)가 임의의 \(\mathbf{v}_1\), \(\mathbf{v}_2 \in V\)에 대해
$$ \left\langle \mathbf{v}_1 , \mathbf{v}_2 \right\rangle _V = \left\langle f\mathbf{v}_1 , f\mathbf{v}_2 \right\rangle _W $$
이면, \(f\)를 \(V\)에서 \(W\)로의 isometry라고 부른다.
By Yves Baelde [CC BY-SA 3.0 ], from Wikimedia Commons
\(V\)와 \(W\)가 finite dimension인 경우 \(T\)가 isometry이고 linear transformation인 경우 \(T\)는 자연스럽게 isomorphism이 된다. 이에 더해 \(T\)는 \(V\)의 orthonormal basis를 \(W\)의 orthonormal basis로 변환한다. 역으로 linear transformation이 \(V\)의 orthonormal basis를 \(W\)의 orthonormal basis로 변환하면 그 transformation은 inner product를 보존하는 isomorphism임이 성립한다. 따라서 finite-dimensional inner product space \(V\)와 \(W\)의 dimension이 같다면 반드시 inner product를 보존하는 isomorphism이 존재한다.
Example
Euclidean space \(\mathbb{C}^n\)의 vector
$$ \mathbf{x}=(x_1,x_2,\cdots,x_n) $$
$$ \mathbf{y}=(y_1,y_2,\cdots,y_n) $$
의 inner product는 보통
$$ \left\langle \mathbf{x} , \mathbf{y} \right\rangle _{\mathbb{C}^n} = \sum_{i=1} ^n x_i y_i ^* $$
으로 정의한다. 이 Inner product는 matrix representation으로도 계산할 수 있다. vector \(\mathbf{x}\)는 standard basis를 이용하여
$$ X = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} $$
의 행렬로 표현한다. 이러한 \(n\times 1\) matrix들의 vector space를 \(\mathbb{C}_{n1}\)이라고 하면 다음과 같이 \(\mathbb{C}_{n1}\)의 inner product를 정의할 수 있다.
$$ \left\langle X , Y \right\rangle _{\mathbb{C}_{n1}} = Y^*X=\sum_{i=1} ^n x_i y_i ^* $$
따라서 matrix representation
$$ \mathbf{x} \to X $$
에 추가적으로 \(\mathbb{C}_{n1}\)에 inner product를
$$ \left\langle X , Y \right\rangle _{\mathbb{C}_{n1}} = Y^*X $$
로 정의하면 matrix representation은 inner product를 보존하는 isomorphism이 된다. 같은 방식으로 finite-dimensional inner product space의 orthonormal basis를 이용한 matrix 표현은 \(\mathbb{C}^{n1}\)로의 inner product를 보존하는 isomorphism이 된다.
Unitary Operator
Inner product space로부터 자기자신으로의 linear transformation인 linear operator가 inner product를 보존하는 isomorphism인 경우 그 operator를 unitary하다고 부른다.
Inner product space \(V\)의 linear operator \(U\)가 임의의 \(\mathbf{v}\), \(\mathbf{w}\in V\)에 대하여
$$ \left\langle U\mathbf{v} , U\mathbf{w} \right\rangle = \left\langle \mathbf{v} , \mathbf{w} \right\rangle $$
을 만족하는 isomorphism인 경우 \(U\)를 unitary operator라고 부른다.
\(U\)가 unitary이면 반드시 Hermitian adjoint \(U^*\)가 존재하고
$$ U^*U=UU^*=I $$
를 만족한다. 경우에 따라 이 조건이 unitary operator의 정의로 사용되기도 하지만 infinite dimensional의 경우 adjoint의 존재가 문제가 될 수 있다. 다만 adjoint의 존재는 space의 정의 문제이므로 위의 조건을 정의로 사용하는 경우가 많다. 주의할 것은 unitary operator는 위의 조건을 만족하는 linear operator라는 것이다. 이 조건을 만족하는 것은 linear operator가 아닌 antiunitary operator도 있다.
Unitary operator는 양자역학 이론에서 핵심적인 역할을 한다. 이는 orthonormal basis가 unitary operator에 의해서 새로운 orthonormal basis로 변환되기 때문이다. Finite-dimensional inner product \(V\)의 orthonormal basis
$$ \mathcal{B}=\{ \mathbf{e}_1, \mathbf{e}_2, \cdots, \mathbf{e}_n \} $$
은 unitary operator \(U\)에 의하여
$$ \left\langle U\mathbf{e}_i , U\mathbf{e}_j \right\rangle = \left\langle \mathbf{e}_i , \mathbf{e}_j \right\rangle = \delta_{ij} $$
이므로
$$ \mathcal{C}=\{ U\mathbf{e}_1, U\mathbf{e}_2, \cdots, U\mathbf{e}_n \} $$
는 새로운 orthonormal basis가 된다.
이제 임의의 operator \(A\)가 \(\mathcal{B}\)에서 matrix 표현이 \([A]_\mathcal{B}\)가 된다면 새로운 orthonormal basis \(\mathcal{C}\)에서 matrix 표현은 (선형대수학) 2.5 Representations of Linear Transformations에서 본 것과 같이
$$ [A]_\mathcal{C} = U^{-1}[A]_\mathcal{B} U = U^*[A]_\mathcal{B} U $$
가 된다. 이를 행렬의 unitary transformation이라고 부른다. 양자역학에서는 \(\left\langle H\psi , \phi \right\rangle\)(물리학과에서 사용하는 표현으로\(\left\langle \phi \left| H \right| \psi \right\rangle\))를 계산하는 상황이 많은데 위의 예제에서 본 것과 같이 orthonormal basis에서 matrix 표현을 통하여 계산할 수 있다. 주어진 basis에서 \(H\), \(\phi\), \(\psi\)의 matrix 표현이 복잡하다면 새로운 orthonormal basis에서 unitary transform된 간단한 matrix 표현으로 계산한다.
'Mathematics > 선형대수' 카테고리의 다른 글
| (선형대수학) 4.6-(3) Example: Special Relativity, Lorentz Transformation (0) | 2018.08.02 |
|---|---|
| (선형대수학) 4.6-(2) Some Spaces Isomorphic to 3-dimensional Euclidean Space (0) | 2018.08.02 |
| (선형대수학) 4.6-(1) Orthogonal Operators (0) | 2018.08.02 |
| (선형대수학) 4.5 Self-adjoint Operators(Hermitian Operators) (1) | 2018.08.02 |
| (선형대수학) 4.4 Hermitian Adjoint of Operators (0) | 2018.08.02 |
| (선형대수학) 4.3 Orthogonality, Gram-Schmidt Process (0) | 2018.08.01 |