이전 페이지에서 살펴본 기대값을 이용하여 불확정성 원리를 확인할 수 있다. 이번 페이지에서는 조화진동자에서 불확정성 원리를 확인해 본다.
#Uncertainty Principle
"양자역학에서 위치와 운동량을 모두 정확히 측정하는 것을 불가능하다"는 불확정성 원리는 수학적으로는 표준편차를 이용해 표현할 수 있다. 확률론에서 어떤 값을 정확히 측정할 수 있다는 것은 표준편차가 0이라는 것과 같으므로 불확정성 원리는 "위치와 운동량의 표준편차를 모두 0으로 만드는 것은 불가능하다"라고 표현할 수 있다.1
THEOREM Uncertainty Principle
\[ \begin{equation} \left( X\text{의 표준편차} \right) \left( P\text{의 표준편차} \right) \ge \frac{\hbar}{2} \label{uncertainty} \end{equation} \]
#Variances of Position and Momentum for a Harmonic Oscillator
확률론에서 분산은 다음과 같이 계산된다.
\[ \text{Var}(A) = E[A^2] - (E[A])^2 \]
따라서, \(X\) 의 분산을 구하기 위해서는 \(X^2\) 의 기대값을 구해야 한다. 이하에서는 계산의 간편함을 위하여 operator를 이용한 기대값 계산 방법을 이용하자.2
\[ X = \sqrt{\frac{\hbar}{2m\omega}} (a+a^\dagger) \]
로부터
\[ \begin{equation} X^2 = \frac{\hbar}{2m\omega} (a+a^\dagger)^2 = \frac{\hbar}{2m\omega} \left[ a^2 + aa^\dagger + a^\dagger a + (a^\dagger)^2 \right] \label{xsquare} \end{equation} \]
주의!! 곱셈 공식 \((x+y)^2 = x^2 + 2xy + y^2\) 과는 다르게 식 \(\eqref{xsquare}\)와 같이 전개되어야 한다. Operator의 경우 일반적으로 \(AB\) 와 \(BA\) 는 같지 않다.
이제 양자수 \(n\) 인 상태에 대하여 \(X^2\)의 기대값을 구해보자.3
\[ E[X^2] = \langle n | X^2 | n \rangle = \frac{\hbar}{2m\omega} (\langle n | aa | n \rangle + \langle n | aa^\dagger | n \rangle + \langle n | a^\dagger a | n \rangle + \langle n | a^\dagger a^\dagger | n \rangle )\]
이제 creation operator와 annihilator operator의 연산
\[ a ~| n \rangle = \sqrt{n} ~| n \rangle \]
\[ a^\dagger ~| n \rangle = \sqrt{n+1} ~| n+1 \rangle \]
을 이용하면,
\[ \langle n | aa | n \rangle = \sqrt{n(n-1)} ~\langle n | n-2 \rangle \]
\[ \langle n | a a^\dagger | n \rangle = (n+1) ~\langle n | n \rangle \]
\[ \langle n | a^\dagger a | n \rangle = n ~\langle n | n \rangle \]
\[ \langle n | a^\dagger a^\dagger | n \rangle = \sqrt{(n+1)(n+2)} ~\langle n | n+2 \rangle \]
여기에 Hamiltonian의 eigenvector들의 orthonormality
\[ \langle n | m \rangle = \delta_{nm} \]
을 적용하면 \(X^2\) 의 기대값을 구할 수 있다.
\[ E[X^2] = \frac{\hbar}{2m\omega} (2n+1) \]
이전 페이지에서 구한 \(E[X]=0\) 을 이용하면, 양자수 \(n\) 인 상태에서 \(X\) 의 분산은 다음과 같이 구할 수 있다.
\[ \text{Var}(X) = E[X^2] - (E[X])^2 = \frac{\hbar}{2m\omega} (2n+1) \]
마찬가지로 양자수 \(n\) 인 상태에서 \(P\) 의 분산을 구하기 위하여
\[ P = i \sqrt{\frac{m\hbar\omega}{2}} (a^\dagger - a) \]
로부터
\[ P^2 = \frac{m\hbar\omega}{2} \left(-aa + aa^\dagger + a^\dagger a - a^\dagger a^\dagger \right) \]
를 이용하면,
\[ \text{Var}(P) = \frac{m\hbar\omega}{2} (2n+1) \]
을 얻을 수 있다.
#Uncertainty of a Harmonic Oscillator
따라서 양자수 \(n\) 인 상태에서 \(X\) 의 표준편차 \(\Delta X\) 와 \(P\) 의 표준편차 \(\Delta P\) 의 값은 각각 다음과 같다.
\[ \Delta X = \sqrt{\text{Var}(X)} = \sqrt{\frac{\hbar}{m\omega}\left( n+\frac{1}{2} \right)} \]
\[ \Delta P = \sqrt{\text{Var}(P)} = \sqrt{m\hbar\omega \left( n + \frac{1}{2} \right)} \]
이로부터 양자수가 \(n\) 인 상태의 조화진동자의 불확정성은
\[ (\Delta X) (\Delta P) = \hbar \left( n+\frac{1}{2} \right) \]
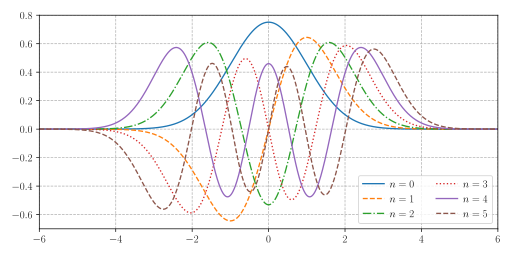
먼저 조화진동자는 불확정성 원리를 만족함을 알 수 있다. 만약 조화진동자가 바닥 상태인 경우, 식 \(\eqref{uncertainty}\)에서 가질 수 있는 최소값인 \(\frac{\hbar}{2}\) 와 동일해진다. 두번째로 조화진동자의 양자수 \(n\) 이 커질수록, 즉, 조화진동자의 에너지 \(E_n = \hbar\omega\left(n+\frac{1}{2}\right)\) 가 커질수록, \(X\) 의 표준편차와 \(P\) 의 표준편차가 커짐을 알 수 있다. 비록 위치와 운동량의 평균(기대값)은 0으로 동일하지만, 에너지가 증가할 수록 위치와 운동량이 0에서 벗어나는 값들의 확률밀도가 증가함을 의미한다. 특히 위치의 경우는 eigenvector의 그래프로부터 직접 확인할 수 있다. 아래 그래프는 몇몇 \(n\) 에 대한 eigenvector \(\psi_n (x)\) 들의 그래프이다. \(n\) 이 증가할 수록 확률밀도 \(\left| \psi_n (x) \right| ^2 \) 가 어떻게 변화하는지 잘 살펴보고 위치의 표준편차가 어떻게 변화하는지 잘 살펴보자.
- 더 일반적인 경우에 대해서는 1.4-(3) Example: 하이젠베르크의 불확정성 원리 Heisenberg's Uncertainty Principle 참고. [본문으로]
- operator를 이용한 방법과 Hermitie polynomial을 직접 이용하는 방법은 표현법만 다를 뿐 본질적으로 같은 연산이다. 이후 나오는 연산은 모두 Hermite polynomial의 적분을 통하여 같은 결론을 얻을 수 있다. [본문으로]
- 기대값을 구하기 위해서는 반드시 상태를 표현해줘야 한다는 것을 명심할 것. [본문으로]