(다양체,텐서) 3.1-(1) Length of Curve

Vector calculus에서 3차원 Euclidean space ${\mathbb{R}}^3$에 정의되는 curve는 1차원 변수 parametrization된다. 예를 들어, 구간

$[0,4\pi ]$에 정의된 함수

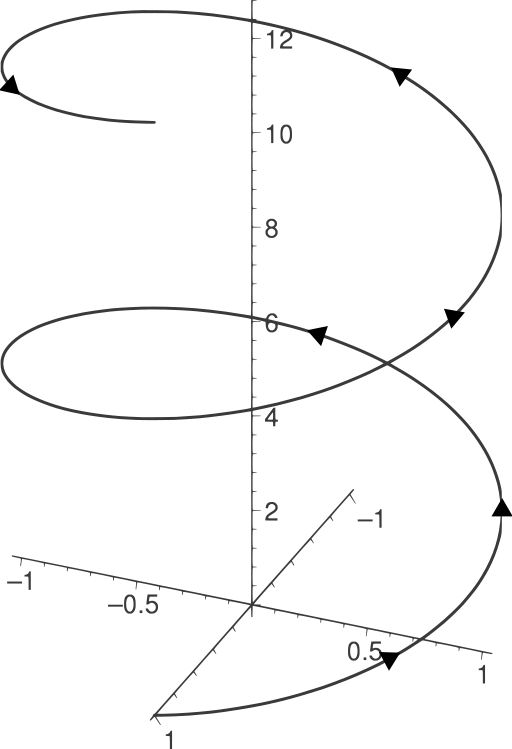
$$\gamma (t)=(\cos t,\sin t,t)$$

는 아래 그림과 같은 형태의 curve가 된다.

By RobHar [Public domain], via Wikimedia Commons

Differentiable curve $\gamma :[a,b]\to {\mathbb{R}}^3$

$$\gamma (t)=(x(t),y(t),z(t))$$

의 길이를 구하기 위해서, $t$가 $t^{\prime }$에서 $t^{\prime }+dt$까지 변하는 동안의 $\gamma$의 작은 조각의 길이를 구해보면, 선형근사

$$\gamma (t^{\prime }+dt)=\gamma (t^{\prime })+\frac{d\gamma }{dt}(dt)=(x(t^{\prime }),y(t^{\prime }),z(t^{\prime }))+(\frac{dx}{dt}(t^{\prime }),\frac{dy}{dt}(t^{\prime }),\frac{dz}{dt}(t^{\prime }))dt$$

이므로, 

$$\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2}$$

임을 알 수 있다. 따라서, $\gamma$의 길이는

$$\mathrm{Length}(\gamma )={\int }_a^b\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2}dt$$

로 구할 수 있다.

이때,

$$\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2}$$

는 $t$에서 curve의 velocity vector

$$\dot{\gamma }(t)=(\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt})$$

의 길이와 같으므로 velocity vector를 tangent vector로, 길이를 Riemannian metric으로 표현하면, manifold에서도 curve의 길이를 다음과 같이 정의할 수 있다.

DEFINITION            The Length of a Curve

Riemannian manifold $(M,⟨\cdot ,\cdot ⟩)$에 대하여, differentiable curve $\gamma :[a,b]\to M$ 의 length를 다음과 같이 정의한다.

$$\mathrm{Length}(\gamma )={\int }_a^b⟨\dot{\gamma }(t),\dot{\gamma }(t)⟩dt$$