2.4-(1) Example: Gradient, Divergence, Curl에서 vector calculus에서 정의된 미분이 exterior derivative와 연관되어 있다는 것을 확인했었다. 이 페이지와 다음 페이지에 걸쳐서 manifold에서 gradient와 divergence를 정식으로 정의하고 local coordinates에서의 표현을 살펴본다. (Curl은 3차원에서만 정의되고 다른 차원에서는 일반화되지 못한다.)
Raising and Lowering Index isomorphism
\(n\)-dimensional smooth manifold \(M\)에 대하여, \(T_pM\)과 \(T_p ^* M\)은 isomorphic하므로, Riemannian metric \(\left\langle \cdot,\cdot \right\rangle\)이 정의되면 [선형대수학] 4.4 Hermitian Adjoint of Operators에서 살펴본 것과 같이
$$ \Phi(v) (w) = \left\langle v , w \right\rangle $$
를 만족하는 isomorphism \(\Phi : T_pM \to T_p ^*M\) 가 존재한다. 이를 모든 점으로 확장하면, vector field와 1-form 사이의 isomorphism \(\Phi : \mathfrak{X}(M) \to \Omega ^1 (M)\) 를 얻을 수 있다. 만약 vector field \(X\)가 local coordinates \(x\)에서
$$ X = \sum_{i=1} ^n X^i \frac{\partial}{\partial x^i} $$
로 표현된다면,
$$ \left\langle X,Y \right\rangle = \sum_{i,j=1} ^n g_{ij}X^i Y^j = \sum_{j=1} ^n \left[ \left(\sum_{i=1} ^n g_{ij}X^i \right) ~dx^j\left(\sum_{k=1} ^n Y^k \frac{\partial}{\partial x^k}\right) \right] = \Phi(X)(Y) $$
이므로 1-form \(\Phi(X)\)는
$$ \Phi(X) = \sum_{j=1} ^n \left(\sum_{i=1} ^n g_{ij}X^i \right) dx^j $$
로 표현된다. Einstein convention을 이용해 coefficient로만 표현하면, 좌변은 1-form이므로 index가 아래에 있으므로
$$ X_i = g_{ij}X^i $$
와 같이 표현된다. (\(X_i\)와 \(X^i\)는 다른 오브젝트를 표현하고 있음에 주의!) Isomorphism \(\Phi\)가 index를 내리는 operator라는 점을 이용해, \(\Phi(X)\) 대신 \(X^\flat\)을 사용하기도 한다.
반대로 \(\Phi^{-1} : \Omega^1(M) \to \mathfrak{X}(M)\) 은 1-form으로부터 vector field를 얻는 map이다. 위와 같은 방식으로, 1-form \(\omega\)가 local coordinates 표현이
$$ \omega = \sum_{i=1} ^n \omega_i ~dx^i $$
이면, \(\Phi^{-1}(\omega)\)는
$$ \Phi^{-1}(\omega) = \sum_{j=1} ^n \left( \sum_{i=1} ^n g^{ij}\omega_i \right) \frac{\partial}{\partial x^j} $$
이다. (\(g^{ij}\)는 \(g_{ij}\)의 역행렬이다.) \(\Phi^{-1}\)은 index를 올리는 operator라는 점으로부터 \(\Phi^{-1}(\omega)\) 대신 \(\omega^{\sharp}\)으로 표현하기도 한다.
Gradients of Functions
Riemannian manifold에서 gradient는 다음과 같이 정의한다.
DEFINITION Gradient of Function (Riemannian)
Riemannian manifold \((M,\left\langle \cdot,\cdot \right\rangle)\)의 smooth function \(f:M \to \mathbb{R}\)의 gradient는 1-form \(df\)의 raising index isomorphism으로 얻어지는 vector field이다.
$$ \mathrm{grad}(f) = \Phi^{-1} (df) $$
Local coordinates \(x\)에서 1-form \(df\)는
$$ df = \sum_{i=1} ^n \frac{\partial f}{\partial x^i} ~dx^i $$
로 표현되므로 \(\mathrm{grad}(f)\)는
$$ \mathrm{grad}(f) = \sum_{j=1} ^n \left( \sum_{i=1} ^n g^{ij} \frac{\partial f}{\partial x^i} \right) \frac{\partial}{\partial x^j} $$
로 표현된다.
Example: Expression of Gradient in Spherical Coordinates
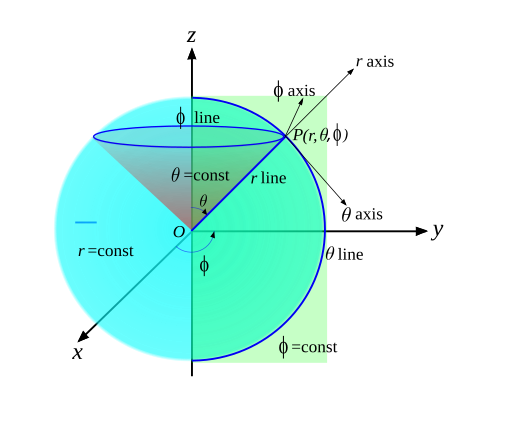
Spherical coordinate system은 interval \([0,\infty]\times[0,\pi]\times[0,2\pi]\)에서 다음과 같이 parametrization된다.
$$ \Psi (r,\theta,\varphi) = (r\sin{\theta}\cos{\varphi},r\sin{\theta}\sin{\varphi},r\cos{\theta}) $$
By Andeggs [Public domain], from Wikimedia Commons
많은 수학과 교재에서는 위의 표현 대신 다음과 같은 parametrization을 택하기도 한다.
$$ \Psi' (r,\theta,\varphi) = (r\sin{\varphi}\cos{\theta},r\sin{\varphi}\sin{\theta},r\cos{\varphi}) $$
By Dmcq [CC BY-SA 3.0 ], from Wikimedia Commons
여기에서는 첫번째 parametrization을 선택하겠다. 이제 point \(p=\Psi(r_0,\theta_0,\varphi_0)\) 에서 tangent space의 basis vector를 얻기 위해 curve \(\gamma_1(t)\), \(\gamma_2(t)\), \(\gamma_3(t)\)를 각각
$$ \gamma_1(t) = \Psi (r_0+t,\theta_0,\varphi_0) \mathrm{~~~~~~~(}r\mathrm{~line~in~the~figure)} $$
$$ \gamma_2(t) = \Psi (r_0,\theta_0+t,\varphi_0) \mathrm{~~~~~~~(}\theta\mathrm{~line~in~the~figure)} $$
$$ \gamma_3(t) = \Psi (r_0,\theta_0,\varphi_0+t) \mathrm{~~~~~~~(}\varphi\mathrm{~line~in~the~figure)} $$
By Lyudmil Antonov Lantonov [GFDL, CC-BY-SA-3.0 or CC BY-SA 2.5 ], via Wikimedia Commons
라고 하면,
$$ \begin{eqnarray} \left(\frac{\partial}{\partial r}\right)_p & = & \left. \frac{d\gamma_1}{dt} \right|_{t=0} & = & \frac{\partial \Psi}{\partial r} (r_0,\theta_0,\varphi_0) & = & (\sin{\theta_0}\cos{\varphi_0},\sin{\theta_0}\sin{\varphi_0},\cos{\theta_0}) \\ \\ \left(\frac{\partial}{\partial \theta}\right)_p & = & \left. \frac{d\gamma_2}{dt} \right|_{t=0} & = & \frac{\partial \Psi}{\partial \theta} (r_0,\theta_0,\varphi_0) & = & (r\cos{\theta_0}\cos{\varphi_0},r\cos{\theta_0}\sin{\varphi_0},-r\sin{\theta_0}) \\ \\ \left(\frac{\partial}{\partial \varphi}\right)_p & = & \left. \frac{d\gamma_3}{dt} \right|_{t=0} & = & \frac{\partial \Psi}{\partial \varphi} (r_0,\theta_0,\varphi_0) & = & (-r\sin{\theta_0}\sin{\varphi_0},r\sin{\theta_0}\cos{\varphi_0},0) \end{eqnarray}$$
Real-valued smooth function \(f(r,\theta,\varphi)\)의 gradient는
$$ \begin{eqnarray} \mathrm{grad}(f) & = & \sum_{j=1} ^n \left( \sum_{i=1} ^n g^{ij} \frac{\partial f}{\partial x^i} \right) \frac{\partial}{\partial x^j} \\ \\ & = & \frac{\partial f}{\partial r} \frac{\partial}{\partial r} + \frac{1}{r^2} \frac{\partial f}{\partial \theta} \frac{\partial}{\partial \theta} + \frac{1}{r^2\sin^2{\theta}} \frac{\partial f}{\partial \varphi} \frac{\partial}{\partial \varphi} \end{eqnarray} $$
이제, tangent space의 basis vector들을 길이로 나눠서 unit vector들을 다음과 같이 정의하자.
$$ \begin{eqnarray} \hat{\mathbf{r}} & = & \frac{\partial}{\partial r} \\ \\ \hat{\mathbf{\theta}} & = & \frac{1}{r} \frac{\partial}{\partial \theta} \\ \\ \hat{\mathbf{\varphi}} & = & \frac{1}{r\sin{\theta}} \frac{\partial}{\partial \varphi} \end{eqnarray} $$
따라서, spherical coordinate에서 \(f(r,\theta,\varphi)\)의 gradient의 표현을 다음과 같이 얻는다.
$$ \mathrm{grad}(f) = \frac{\partial f}{\partial r} \hat{\mathbf{r}} + \frac{1}{r} \frac{\partial f}{\partial \theta} \hat{\mathbf{\theta}} + \frac{1}{r\sin{\theta}} \frac{\partial f}{\partial \varphi} \hat{\mathbf{\varphi}} $$
'Mathematics > 다양체(텐서)' 카테고리의 다른 글
| [다양체,텐서] 3.2-(1) Torsion Tensors (0) | 2018.09.15 |
|---|---|
| [다양체,텐서] 3.2 Affine Connections, Covariant Derivatives (2) | 2018.09.15 |
| [다양체,텐서] 3.1-(3) Divergence of Vector Field (0) | 2018.09.14 |
| (다양체,텐서) 3.1-(1) Length of Curve (0) | 2018.09.13 |
| [다양체,텐서] 3.1 Riemannian Metric (0) | 2018.09.11 |
| [다양체,텐서] 2.7 Stokes' Theorem (0) | 2018.09.09 |