Euclidean space에서는 유클리드 기하학의 공리들로부터, 하나의 직선을, 교차하는 다른 curve 위에서 평행하게 옮기는 것이 가능하다. Affine connection이 정의된 manifold에서도 이러한 것이 가능한데 이를 parallel transport라고 부른다.
Parallel Vector Field along a Curve
Affine connection \(\nabla\)가 정의된 manifold \(M\)의 differentiable curve \(\gamma:I\to M\)에 대하여, map \(X: I \to TM\)
$$ X(t) \in T_{\gamma(t)}M $$
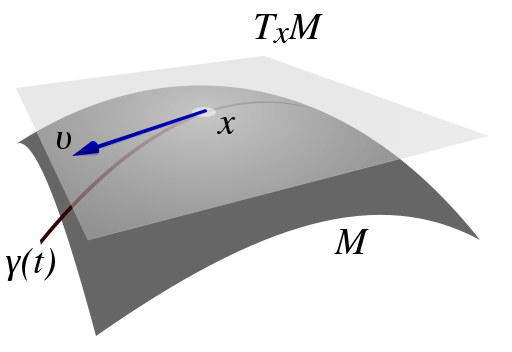
를 \(\gamma\) 에 정의된 vector field라고 부른다. 가장 대표적인 예가 curve의 tangent vector \(\dot{\gamma}(t)\)이다. \(\gamma(t)\)가 시간을 매개변수로 하는 입자의 이동경로라고 한다면, \(\dot{\gamma}(t)\) (아래 그림에서 \(v\) )는 각 위치에서의 속도를 표현한다고 생각할 수 있다.
By derivative work: McSush (talk)Tangentialvektor.png: TNThe original uploader was TN at German Wikipedia. (Tangentialvektor.png) [Public domain],
이제 curve 위의 vector field가 curve 위에서 평행하다는 것을 다음과 같이 정의한다.
DEFINITION Parallel Vector Field along Curve
Affine connection \(\nabla\)가 정의된 manifold \(M\)의 differentiable curve \(\gamma\)에 대하여, \(\gamma\)에 정의된 vector field \(X\)가
$$ \nabla _{\dot{\gamma}(t)} X = 0 $$
이면, \(X\)가 \(\gamma\) 를 따라 parallel하다고 부른다.
만약 \(\gamma(0)\)에서 tangent vector \(A\)에 대하여,
$$ \nabla _{\dot{\gamma}(t)} X = 0 $$
$$ X_{\gamma(0)} = A $$
를 만족하는 \(\gamma\)에 정의된 vector field \(X\)를 tangent vector \(A\)의 \(\gamma\)를 따라서 parallel transport한 vector field라고 부른다.
Local coordinates \(x=(x^1,x^2,\cdots,x^n)\)에서 위의 식은
$$ \dot{X}^i (t) + \sum _{j,k=1} ^n \Gamma ^i _{jk} (\gamma(t)) ~\dot{x}^j(t)X^k(t) = 0 $$
$$ X^i (0) = A^i \ $$
즉, ODE와 initial value로 표현된다. Picard-Lindelöf theorem(--DE,theorem-- 참고)에 따라 solution \(X\)가 유일하게 존재한다.
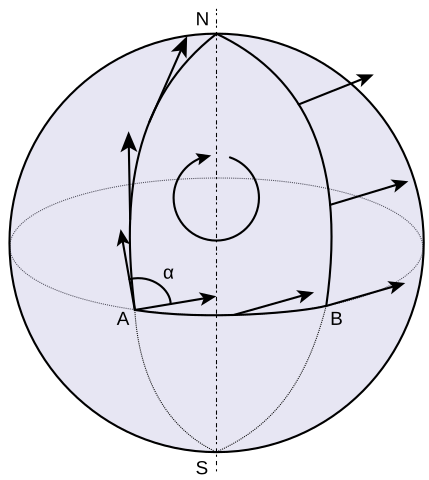
아래의 그림은 구 표면에 정의된 curve를 따라서 parallel transport한 것을 표현한 것이다.
By Fred the Oyster [CC BY-SA 4.0 ], via Wikimedia Commons
점 A에서 북쪽을 가르키고 있는 tangent vector가 N까지 이어진 curve를 따라 parallel transport되고, 다시 B까지 이어진 curve를 따라 parallel transport, 다시 A까지 이어진 curve를 따라 parallel transport된 결과를 보여주고 있다. Euclidean space에서는 한 점으로 돌아오는 curve를 따라 parallel transport를 하면, 원래의 vector가 되는데, 그림에서와 같이 일반적인 manifold에서는 그렇지 않다는 것을 알 수 있다.
Geodesics
3차원 공간에서 어떠한 외력을 받지 않는 입자의 운동은 직선으로 나타난다. 입자가 움직이는 경로를 따라 입자의 속도를 체크하면, 속도가 직선을 따라 parallel transprot함을 알 수 있다. 이를 일반화한 개념이 geodesic이다.
DEFINITION Geodesic of Manifold
Affine connection \(\nabla\)가 정의된 manifold \(M\)의 curve \(\gamma:I\to M\)이
$$ \nabla _{\dot{\gamma}(t)} \dot{\gamma}(t) = 0 $$
를 (affine) geodesic이라고 부른다.
Local coordinates 표현은
$$ \ddot{x}^i + \sum_{j,k=1} ^n \Gamma ^i _{jk} ~\dot{x}^j ~\dot{x}^k = 0 $$
으로 2차 ODE가 된다. 만약 initial value \(\gamma(0)=p\), \(\dot{\gamma}(0)=v \in T_pM\)이 주어진다면, Picard-Lindelöf theorem에 의하여 solution이 유일하게 결정된다.
'Mathematics > 다양체(텐서)' 카테고리의 다른 글
| [다양체,텐서] 3.5 Exponential Maps, Normal Coordinates (0) | 2018.10.06 |
|---|---|
| [다양체,텐서] 3.4-(1) Example: Geometry on Unit Sphere (0) | 2018.10.05 |
| [다양체,텐서] 3.4 Levi-Civita Connection (0) | 2018.10.05 |
| [다양체,텐서] 3.2-(2) Coordinates Changes of Christoffel Symbols (0) | 2018.09.26 |
| [다양체,텐서] 3.2-(1) Torsion Tensors (0) | 2018.09.15 |
| [다양체,텐서] 3.2 Affine Connections, Covariant Derivatives (2) | 2018.09.15 |