반지름이 1인 구표면의 Levi-Civita connection과 여기로부터 얻어지는 구표면에서의 기하학에 대하여 살펴보자.
The Levi-Civita Connection on Sphere
3.1-(2) Gradient of Function의 예제에서 살펴본 것과 같이 구표면에 대한 parametrization을
$$ \Psi (\theta,\varphi) = (\sin\theta \cos\varphi , \sin\theta \sin\varphi, \cos\theta) $$
로 택하면, Riemannian metric과 그 inverse를 구해보면,
$$ \begin{eqnarray} g & = & \left( \begin{array}{cc} 1 & 0 \\ 0 & \sin^2{\theta} \end{array} \right) \\ \\ g^{-1} & = & \left( \begin{array}{cc} 1 & 0 \\ 0 & 1/\sin^2{\theta} \end{array} \right) \end{eqnarray} $$
이다. 따라서 Levi-Civita connection의 Christoffel symbol은
$$ \begin{eqnarray} \Gamma ^\theta _{\varphi \varphi} & = & -\sin\theta \cos\theta \\ \\ \Gamma ^\varphi _{\theta \varphi} & = & \cot\theta \\ \\ \Gamma ^i _{jk} & = & 0 \mathrm{~~,~~for~other~index} \end{eqnarray} $$
을 얻을 수 있다.
Geodesics on Sphere: Great Circles
이제 geodesic equation을 구하면,
$$ \ddot{\theta} - \dot{\varphi}^2 \sin\theta \cos\theta = 0 $$
$$ \ddot{\varphi} + 2 \dot{\theta}\dot{\varphi} \cot\theta = 0 $$
다음과 같이 정의되는 구표면 상의 curve
$$ \begin{eqnarray} \theta(t) & = & \frac{\pi}{2} \\ \\ \varphi(t) & = & 2\pi t \end{eqnarray} $$
는 위의 geodesic equation을 만족함을 알 수있다. (이 curve를 equator(적도)라고 부른다. 아래 그림 참고)
Reference: NASA
구표면은 회전에 대하여 대칭이기 때문에, 임의의 great circle (원점을 중심으로 구표면에 그려지는 반지름 1의 원)은 geodesic임을 알 수 있다.
Internal Angles in Triangles
유클리드 기하학에서 삼각형을 세 직선으로 갇힌 도형이라고 한다면, Riemannian manifold로 개념을 확장하여 삼각형을 세 geodesic으로 갇힌 도형으로 생각할 수 있다. 이제 구표면에서 great circle(또는 그 일부) 3개를 생각해보자.
1. 적도
2. 경도 0에서 자오선
3. 경도 90에서 자오선
이렇게 그려지는 삼각형의 내부 각도는 모두 90도가 된다. 따라서 삼각형 내각의 합이 270이 된다. 따라서 구표면에서의 기하학에서는 유클리드 기하학과는 다른 결론을 얻는다.
The Parallel Postulate, Playfair's axiom
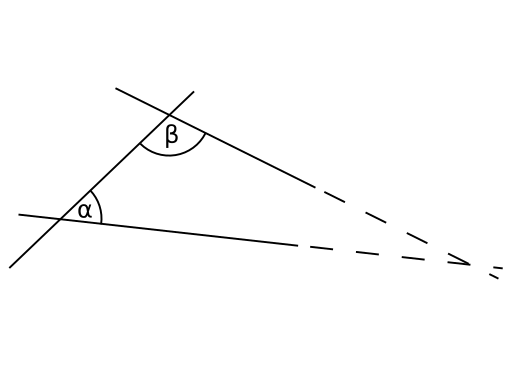
사실, 삼각형 내각의 합이 180도 라는 명제는 유클리드 기하학의 마지막 공준인 parallel postulate(평행선 공준)과 동치이다. 따라서 구표면에서의 기하학은 parallel postulate가 성립하지 않는다. Parallel postulate 내용은 다음과 같다.
두 직선이 다른 한 직선과 만나 이루는 두 동측내각의 합이 두 직각보다 작다면, 이 두 직선을 무한히 연장할 때, 그 두 동측내각과 같은 쪽에서 만난다.
By 6054 [GFDL or CC-BY-SA-3.0], via Wikimedia Commons
이와 동등한 명제로 유명한 것은 Playfair's axiom이다.
주어진 직선 밖에 있는 한 점을 지나는 평행선은 유일하게 존재한다.
Playfair's axiom은 구표면의 기하학에서는 성립하지 않는다. 예를 들어, 적도와 적도 밖에 있는 북극에 대하여 명제를 검증해보면, 북극을 지나는 geodesic인 자오선은 반드시 적도를 지나기 때문에 평행선이라는 것이 존재하지 않는다.
'Mathematics > 다양체(텐서)' 카테고리의 다른 글
| [다양체,텐서] 3.5-(1) Lie Groups, Lie Algebras ② (1) | 2018.10.08 |
|---|---|
| [다양체,텐서] 3.5-(1) Lie Groups, Lie Algebras ① (0) | 2018.10.07 |
| [다양체,텐서] 3.5 Exponential Maps, Normal Coordinates (0) | 2018.10.06 |
| [다양체,텐서] 3.4 Levi-Civita Connection (0) | 2018.10.05 |
| [다양체,텐서] 3.3 Parallel Transport, Geodesics (0) | 2018.09.26 |
| [다양체,텐서] 3.2-(2) Coordinates Changes of Christoffel Symbols (0) | 2018.09.26 |