[양자역학] 3.2 에르미트 다항식 Hermite Polynomials

지난 페이지에서는 harmonic oscillator의 energy가

$$E=(n+\frac{1}{2})\hslash \omega ,n=0,1,2,\cdots$$

만 가능하다는 것을 살펴보았다. 이번 페이지에서는 Hamiltonian operator의 eigenvector에 대하여 알아본다.

#Hermite Polynomials

지난 페이지에서

$$u(y)=C_0[1+\frac{1-2ϵ}{2\cdot 1}{y}^2+\frac{1-2ϵ}{2\cdot 1}\frac{5-2ϵ}{4\cdot 3}{y}^4+\cdots ]+C_1[y+\frac{3-2ϵ}{3\cdot 2}{y}^3+\frac{3-2ϵ}{3\cdot 2}\frac{7-2ϵ}{5\cdot 4}{y}^3+\cdots ]$$

최고차항 $n$이 홀수일 일 때는 $C_0$를 0, 짝수일 때는 $C_1$을 0으로 하고 다른 값은 적당히 잡아 얻게되는 다항식들을 Hermite polynomials (of the first kind)라고 부른다.

$$\begin{array}{ccl}{H}_0(y)& =& 1\\ H_1(y)& =& 2y\\ H_2(y)& =& 4y^2-2\\ H_3(y)& =& 8y^3-12y\\ H_4(y)& =& 16y^4-48y^2+12\end{array}$$

확률론에서는 다음과 같이 정의하기도 한다.

$$\begin{array}{ccl}H{e}_0(x)& =& 1\\ H{e}_1(x)& =& x\\ H{e}_2(x)& =& x^2-1\\ H{e}_3(x)& =& x^3-3x\\ H{e}_4(y)& =& x^4-6x^2+3\end{array}$$

자세한 형태는 다르지만 $x=\sqrt{2}y$와 상수$2^{\frac{n}{2}}$를 곱해줌으로써 서로 얻을 수 있다. 예를 들어, $H_3(y)=2\sqrt{2}H{e}_3(\sqrt{2}y)$가 성립한다. 따라서 $H$와 $He$는 사실상 같은 다항식 카테고리에 들어간다고 할 수 있다. 다음 그림은 처음 6개의 Hermite polynomial들의 그래프이다.

Hermite_poly_solid.svg: *Hermite_poly.svg: Alessio Damatoderivative work: Vulpecula (talk)

This W3C-unspecified plot was created with Gnuplot.derivative work: Vulpecula / CC BY-SA

#Properties of Hermite Polynomials

1. Rodrigues' Formula

Hermite polynomials는 다음과 같은 식으로 얻어진다.

THEOREM            Rodrigues' Formula for Hermite Polynomials

$$H_n(y)=(-1{)}^n{e}^{y^2}\frac{d^n}{d{y}^n}{e}^{-y^2}$$

2. Orthogonality

$m<n$일 때, 적분

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-y^2}{H}_m(y)H_n(y)dy$$

를 계산해보자. Rodrigues' Formula로부터,

$$e^{-y^2}{H}_n(y)=(-1{)}^n\frac{d^n}{d{y}^n}{e}^{-y^2}$$

이므로 적분식은

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{H}_m(y)\frac{d^n{e}^{-y^2}}{d{y}^n}dy$$

이제 integral by part를 적용하면,

$${[H_m(y)\left(\frac{d^{n-1}}{d{y}^{n-1}}{e}^{-y^2}\right)]}_{-\mathrm{\infty }}^{\mathrm{\infty }}-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\left(\frac{d}{dy}{H}_m\right)\left(\frac{d^{n-1}}{d{y}^{n-1}}{e}^{-y^2}\right)dy$$

이 때, 첫번째 항의 미분은

$$\frac{d^{n-1}}{d{y}^{n-1}}{e}^{-y^2}=\text{(다항식)}\cdot e^{-y^2}$$

이므로 결국 첫번째 항은 boundary에서 $e^{-y^2}$에 의해 0이 된다. 이렇게 integral by part를 계속하면,

$$(-1{)}^{m+n}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(\frac{d^n}{d{y}^n}{H}_m(y))e^{-y^2}dy$$

를 얻는다. 그러나 $m<n$이므로 $m$차 다항식 $H_m$을 $n$번 미분하면 0이므로 적분식은 0이된다.

만약 $m=n$일 때는 integral by part의 결과는

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}(\frac{d^n}{d{y}^n}{H}_n(y))e^{-y^2}dy$$

이 된다. $\frac{d^n}{d{y}^n}{H}_n(y)$는 $\text{(}최고차항의계수)\times n!$이고 최고차항의 계수는 Rodrigues' Formula로부터 $2^n$임을 쉽게 구할 수 있다. 이를 정리하면 다음과 같다.

THEOREM            Orthogonal Property of Hermite Polynomials

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{e}^{-y^2}{H}_n(y)H_m(y)dy=2^{n}n!\sqrt{\pi }{\delta }_{mn}=\{\begin{array}{cc}{2}^{n}n!\sqrt{\pi }& \text{if }n=m\\ 0& \text{otherwise}\end{array}$$

3. Useful Relations

Hermite polynomial들은 다음과 같은 식을 만족한다.

THEOREM            Recurrence Relations Between Hermite Polynomials

$$H_n^{\prime }(y)=2n{H}_{n-1}(y)$$

$$H_{n+1}(y)=2y{H}_n(y)-2n{H}_{n-1}(y)$$

THEOREM            Explicit Expression of Hermite Polynomials

$$H_n(y)=n!\sum _{m=0}^{\lfloor \frac{n}{2}\rfloor }\frac{(-1{)}^m}{m!(n-2m)!}(2x{)}^{n-2m}=\{\begin{array}{ll}n!\sum _{l=0}^{\frac{n}{2}}\frac{(-1{)}^{\frac{n}{2}-l}}{(2l)!(\frac{n}{2}-l)!}(2x{)}^{2l}& \text{for even }n\\ n!\sum _{l=0}^{\frac{n-1}{2}}\frac{(-1{)}^{\frac{n-1}{2}-l}}{(2l+1)!(\frac{n-1}{2}-l)!}(2x{)}^{2l+1}& \text{for odd }n\end{array}$$

#Solutions of Schrödinger Equation

이제 Schrödinger equation의 해

$${\psi }_n(y)=H_n(y)e^{\frac{-y^2}{2}}$$

에 대하여 inner product를 구하면

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\psi }_n^{\ast }(y){\psi }_n(y)dy=2^{n}n!\sqrt{\pi }$$

이므로 inner product가 1이 되도록 하기위해 적당한 상수를 곱하고, 원래 변수 $x$로 돌아오기 위해 $y={\left(\frac{m\omega }{\hslash }\right)}^{\frac{1}{2}}x$ 를 대입하면 다음을 얻는다.

THEOREM            Solutions of Harmonic Oscillator

 

Harmonic oscillator의 Hamiltonian operator

$$H=\frac{P^2}{2m}+\frac{1}{2}m{\omega }^2{x}^2$$

의 eigenvalue $E=(n+\frac{1}{2})\hslash \omega$에 대한 eigenvector는

$${\psi }_n(x)={\left(\frac{m\omega }{2^{2n}(n!{)}^2\pi \hslash }\right)}^{\frac{1}{4}}{H}_n\left[{\left(\frac{m\omega }{\hslash }\right)}^{\frac{1}{2}}x\right]e^{(-\frac{m\omega }{2\hslash }{x}^2)}$$

이다. 보통 vector의 성질과 quantum number $n$을 강조하기 위하여 ${\psi }_n(x)$ 대신 $|n⟩$으로 쓴다.

Harmonic oscillator에서 Hamiltonian operator의 eigenvector은 서로 orthonormal하다. 즉,

$$⟨n|m⟩={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\psi }_n^{\ast }(x){\psi }_m(x)dx={\delta }_{nm}$$

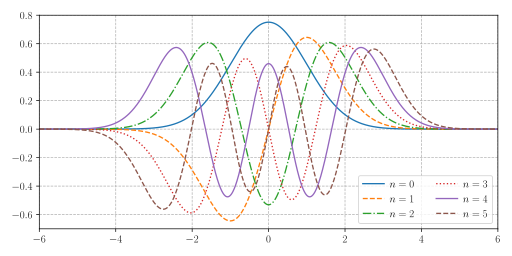
다음 그림은 처음 6개 eigenvector들의 그래프이다.

[n=0(검정), 1(빨강), 2(파랑), 3(노랑), 4(초록), 5(분홍)] MaciejDems / Public domain via Wikimedia

#Completeness

2.1 상자 속 입자 A Particle in a Box ②에서 Schrodinger equation의 eigenvector들이 basis vector처럼 작용해서 일반적인 wave function을 eigenvector들로 전개할 수 있다. 이러한 성질은 harmonic oscillator에서도 마찬가지이다. 이를 eigenvector들이 complete하다고 부른다. 양자역학의 무대가 되는 무한차원 vector space에서 이를 증명하는 것은 해석학적 개념들이 필요하므로 생략한다.

또한, harmonic oscillator의 eigenvector 역시 서로 orthonormal하기 때문에 일반적인 wave function $|f⟩$이

$$|f⟩=\sum _{n=0}^{\mathrm{\infty }}{c}_n|n⟩$$

로 전개되었을 때, 계수 $c_n$는 $|f⟩$와 $|n⟩$의 inner product로 구할 수 있다.

$$c_m=⟨m|f⟩={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\psi }_m^{\ast }(x)f(x)dx$$

#Linear Algebra

양자역학의 나오는 식들을 이해하기 위해서는 orthogonality, completeness를 적분으로만 생각하지 말고 vector 관점에서 생각해야 한다.

① 주어진 $W(x)$에 대하여, 함수 $f(x)$ 가 다음 적분이 가능한 경우, $f(x)$ 는 벡터다.

$${\int }_{\text{domain}}W(x)f^{\ast }(x)f(x)dx$$

② 위에서 주어진 $W(x)$에 대하여, 다음 적분은 벡터 $f(x)$와 $g(x)$의 내적이다.

$${\int }_{\text{domain}}W(x)f^{\ast }(x)g(x)dx$$

③ Orthogonality는 두 벡터를 내적해서 0, 즉 서로 직각이라는 의미를 가진다.

④ Completeness는 그 벡터들이 basis가 될 수 있다는 뜻이다.

Hermite Polynomial이 orthogonal하고 complete하므로 결국 직각인 basis, 직교 좌표계의 basis 벡터와 같은 방식으로 다룰 수 있다. 2.1 상자 속 입자 A Particle in a Box ② 내용을 꼭 살펴보고 이해할 것.