[양자역학] 1.4-(1) Example: 슈테른-게를라흐 실험 Stern-Gerlach Experiment

양자역학에서 측정은 고전역학에서 측정에서 기대되는 것과는 전혀 다른 현상이 도출된다. 대표적인 예로 Stern-Gerlach 실험이 있다.

#Stern-Gerlach Experiment

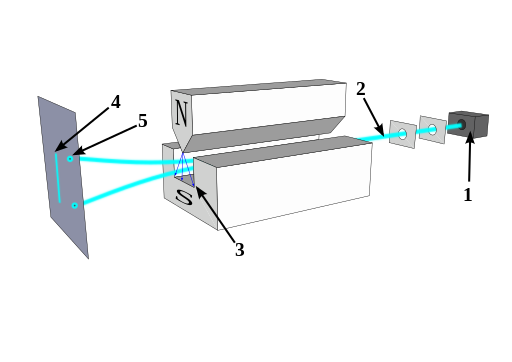
Stern-Gerlach 실험은 아래 그림과 같이 균일하지 않은 magnetic field에 은 원자빔을 통과시켜서 은 원자의 스핀을 구분하는 실험이다.

By Tatoute [CC BY-SA 4.0 ], from Wikimedia Commons

스핀은 입자에 주어지는 angular momentum의 일종으로 고전역학적으로는 기술되지 않는 현상이다. 고전역학에서 angular momentum은 임의의 모든 값이 가능하기 때문에 그림에서 4번과 같은 결과가 기대되지만, 실제 실험에서는 5번과 같이 2개의 값만이 검출된다. 스핀에 대한 자세한 내용은 4.7 스핀 Spin에서 살펴볼 것이다.

은 원자의 스핀은 2차원 vector space에서 기술된다. 위의 실험은 observable $S_z$ 로 표현되며, 위쪽으로 휘는 빔을 측정값 $\frac{\hslash }{2}$ 와 state vector $|\uparrow ⟩$ 로 표현하고 up spin이라고 부르며, 아래쪽으로 휘는 빔을 측정값 $-\frac{\hslash }{2}$ 와 state vector $|\downarrow ⟩$ 로 표현한고 down spin이라고 부른다. 

이 기구를 빔의 진행축을 중심으로 90도 돌려서 실험하는 경우 빔이 좌우로 갈라지게 된다. 이렇게 90도를 돌려서 하는 측정을 observable $S_x$ 로 표현하고, 오른쪽으로 휘는 빔을 측정값 $\frac{\hslash }{2}$ 와 state vector $|\to ⟩$ , 왼쪽으로 휘는 빔을 측정값 $-\frac{\hslash }{2}$ 와 state vector $|\leftarrow ⟩$ 로 표현한다.

#Basic Theory of Spin

1.4 측정, 확률 Measures, Probabilities에서 논의한 것과 같이, Hermitian operator $S_z$ 의 eigenvector $|\uparrow ⟩$ 와 $|\downarrow ⟩$ 은 은 원자의 스핀을 기술하는 2차원 vector space의 basis가 된다. 똑같이 Hermtian operator $S_x$의 eigenvector $|\leftarrow ⟩$ , $|\to ⟩$ 역시 basis가 된다. 임의의 vector들은 basis vector들의 linear combination으로 표현되는데, up spin과 down spin 역시 vector이므로 $S_x$ 의 eigenvector들로 표현될 수 있다. 마찬가지로 $|\to ⟩$ 역시 $S_z$ 의 eigenvector들로 표현된다. 4.7 스핀 Spin에 의하면

$$\begin{array}{rclrclr}|\uparrow ⟩& =& \frac{1}{\sqrt{2}}& |\to ⟩& +& \frac{1}{\sqrt{2}}& |\leftarrow ⟩\\ \\ |\to ⟩& =& \frac{1}{\sqrt{2}}& |\uparrow ⟩& +& \frac{1}{\sqrt{2}}& |\downarrow ⟩\end{array}$$

의 관계가 있다.

#Sequential Experiments

Stern-Gerlach 실험을 다음과 같이 연속적으로 해보자.

1. 은 원자빔에 $S_z$ 측정 후, 위쪽 빔을 선택하여 다시 $S_z$ 측정

2. 은 원자빔에 $S_z$ 측정 후, 위쪽 빔을 선택하여 $S_x$ 측정

3. 은 원자빔에 $S_z$ 측정 후, 위쪽 빔을 선택하여 $S_x$ 측정 후, 오른쪽 빔을 선택하여 $S_z$ 측정

By Francesco Versaci [Public domain], from Wikimedia Commons

고전역학적 직관으로 실험 결과를 예상하면,

1. $S_z$ 측정 후 위쪽 빔을 선택하여 다시 $S_z$ 를 측정하면 위쪽 빔만 나올 것이다.

2. $S_z$ 측정 후 위쪽 빔을 선택한 것은 좌우와는 무관하므로, 위쪽 빔을 선택하여 $S_x$ 를 측정하면 50%는 오른쪽으로, 50%는 왼쪽으로 빔이 분리될 것이다.

3. $S_z$ 측정에서 위쪽으로 휘는 빔을 선택했고 $S_x$ 측정에서 오른쪽으로 휘는 빔을 선택했으므로, 다시 $S_z$ 를 측정하면 빔이 위쪽으로만 휠 것이다.

그러나 실제 실험 결과는 다르다.

3. $S_z$ 측정 후 위쪽 빔을 선택하여 $S_x$ 측정 후, 오른쪽 빔을 선택하여 $S_z$ 를 측정하면 50%는 위쪽으로, 50%는 아래쪽으로 빔이 분리된다.

#Quantum Mechanical Description

이를 양자역학적으로 해석해보자. 2번 실험의 결과는 다음 그림처럼 표현 가능하다.

$$\text{initial beam }|\psi ⟩\underset{\text{select upward beam}}{\overset{S_z}{\to }}|\uparrow ⟩\underset{\text{select rightward beam}}{\overset{S_x}{\to }}|\to ⟩$$

일반적인 하나의 은 원자빔 $|\psi ⟩$ 는 basis vector의 linear combination

$$|\psi ⟩=a|\uparrow ⟩+b|\downarrow ⟩$$

이므로 $S_z$ 측정시에 $\frac{{\left|a\right|}^2}{{\left|a\right|}^2+{\left|b\right|}^2}$ 의 확률로 위쪽으로 휘고 $\frac{{\left|b\right|}^2}{{\left|a\right|}^2+{\left|b\right|}^2}$ 의 확률로 아래쪽으로 휘게 된다. 이중에서 위쪽으로 휘는 빔을 선택하는 것은 state vector가 $|\psi ⟩$ 에서 $|\uparrow ⟩$ 로 wave function collapse된 빔을 선택한 것이다.

이렇게 collapse된 state vector에 $S_x$ 를 측정하면,

$$|\uparrow ⟩=\frac{1}{\sqrt{2}}|\to ⟩+\frac{1}{\sqrt{2}}|\leftarrow ⟩$$

이므로 50% 확률로 오른쪽으로 휘고, 50% 확률로 왼쪽으로 휘게 된다. 이중에서 오른쪽으로 휘는 빔을 선택하는 것은 state vector를 $|\uparrow ⟩$ 에서 $|\to ⟩$ 로 collapse된 빔을 선택한 것이다.

이제 $|\to ⟩$ 로 collapse된 state vector에 $S_z$ 를 측정하면,

$$|\to ⟩=\frac{1}{\sqrt{2}}|\uparrow ⟩+\frac{1}{\sqrt{2}}|\downarrow ⟩$$

이므로 50% 확률로 위쪽으로, 50% 확률로 아래쪽으로 휜다는 결론을 얻게 된다.

양자역학은 고전역학적 직관으로 생각했을 때 이상해 보이는 결론을 도출한다. 이러한 결론이 우리의 직관과 어긋난다고 해서 양자역학이 옳냐 그르냐 판단하는 것이 아니라, 실제 우주가 양자역학이 가정하는 물리체계를 따른다는 것을 이해해야 할 것이다.